Optionen - die Königsklasse der Trading-Instrumente - Teil 3

Bevor wir das Thema der „Besicherung“ jedoch konkret besprechen, müssen wir noch einmal auf die Entwicklungsmöglichkeiten des Deltas eingehen und damit an die Aussagen der Artikel 1 und 2 dieser Serie anknüpfen.

Fassen wir somit noch einmal kurz zusammen:

- Der Wert einer Option verändert sich in der Regel nicht liniear zur Wertveränderung des jeweiligen Basiswertes, wodurch sich eine Option von anderen Finanzinstrumenten abhebt. Der Grund für diese abweichende Wertveränderung liegt einzig und allein darin begründet, dass eine Option für den Käufer nur ein Ausübungsrecht darstellt (keine Verpflichtung, den Basiswert zu beziehen und diesen dann auch bezahlen zu müssen).

- Diese Kennziffer, mit der wir die Wertveränderung der Option im Vergleich zur Wertveränderung des Basiswertes darstellen, nennen wir „DELTA“. Ganz praktisch und pragmatisch können wir sagen: das Delta sagt uns auch etwas aus über die Wahrscheinlichkeit der Ausübung einer Option. Ist die Option rechnerisch gesehen mit einer 100 prozentigen Eintrittswahrscheinlichkeit KEINE Ausübung, ist ihr Delta Null. Ist die Option dagegen eine 100 prozentige Ausübung, ist ihr Delta Eins. Alles dazwischen zeigt eine nachlassende oder zunehmende Wahrscheinlichkeit der Ausübung an. Den Zusammenhang dieser Kenngröße in Abhängigkeit der Faktoren Zeit und Volatilität haben wir in den beiden vorangegangenen Artikeln besprochen.

- Da eine Kaufoption (der Call) das Recht (nicht die Pflicht) zum Erwerb des Basiswertes zu einem bestimmten Basispreis innerhalb einer festgelegten Bezugszeitspanne (amerikanische Optionen) oder zu einem festgesetzten Bezugszeitpunkt (europäische Optionen) definiert, sinkt ihr Delta, je geringer ihre Ausübungswahrscheinlichkeit wird, wenn der Preis des Basiswertes fällt. Eine Verkaufsoption (der Put) ist das Recht (nicht die Pflicht), den Basiswert zu einem bestimmten Basispreis zu verkaufen (auch hier gibt es amerikanische und europäische Optionen). Das Delta des Puts verändert sich ebenfalls in Abhängigkeit der Ausübungswahrscheinlichkeit, wenn sich der Preis des Basiswertes verändert. Steigt dieser, sinkt diese naturgemäß, somit geht auch das Delta zurück.

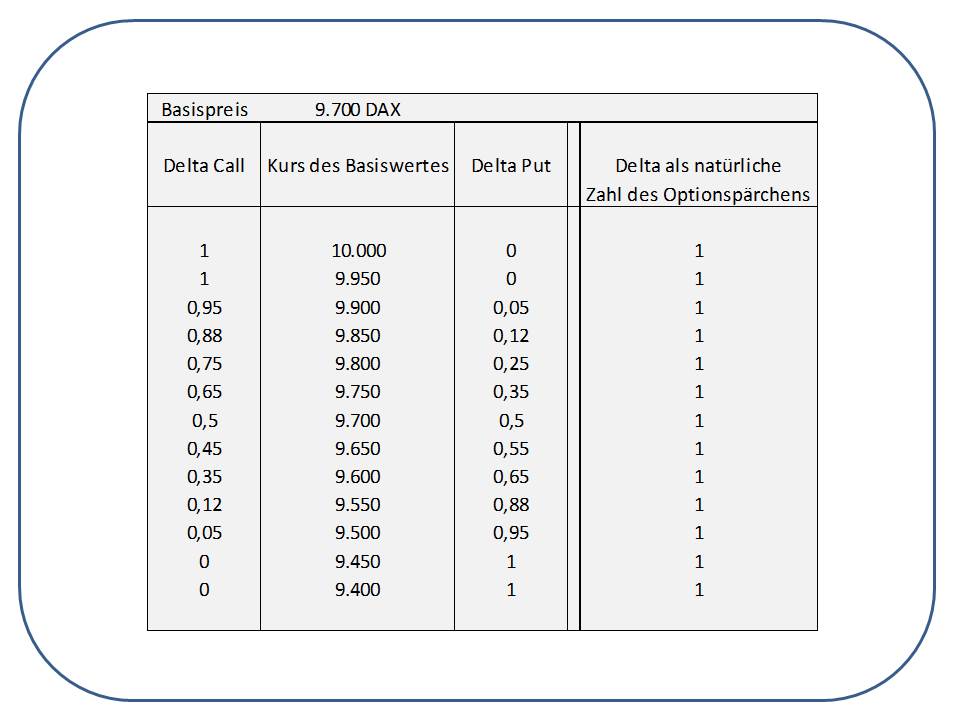
Dieser Sachverhalt hat folgenden Effekt: das Delta des Calls und das Delta des Puts eines Basispreises (also ein Optionspärchen) haben in der Summe immer ein Delta von EINS (sofern wir das Delta jetzt als natürliche Zahl unterstellen). Warum ist das so? Wenn die Wahrscheinlichkeit einer Call-Ausübung mathematisch gesehen bei 100 Prozent liegt, läge naturgemäß die Ausübungswahrscheinlichkeit eines Puts bei 0 Prozent. Sinkt die Wahrscheinlichkeit der Call-Ausübung ab, steigt natürlich im Gegenzug die Ausübungswahrscheinlichkeit des Puts, nämlich in dem Umfang, wie diese beim Call abnimmt. Hat der Call nur noch eine 80 prozentige Ausübungswahrscheinlichkeit (Delta von 0,8), liegt diese des Puts bereits bei 20 Prozent (Delta von 0,2). Es ist völlig egal, wo das Delta des Calls ausgewiesen wird, das Delta des Puts steht diesem immer in der Höhe gegenüber, um in der Summe beider natürlichen Zahlen die 1 zu ergeben.

Dieser Sachverhalt ist für das Verständnis einer Option sehr wichtig und soll in der nachfolgenden Tabelle widergespiegelt werden.

Dieser Aspekt muss unbedingt bei der Bewertung eines Open-Interest im Markt beachtet werden. Ohne das Verständnis dieses Sachverhaltes, werden die wirklichen Auswirkungen auf den Markt durch ein bestehendes Open-Interest falsch interpretiert. Dazu werde ich am Ende des Artikels konkret.

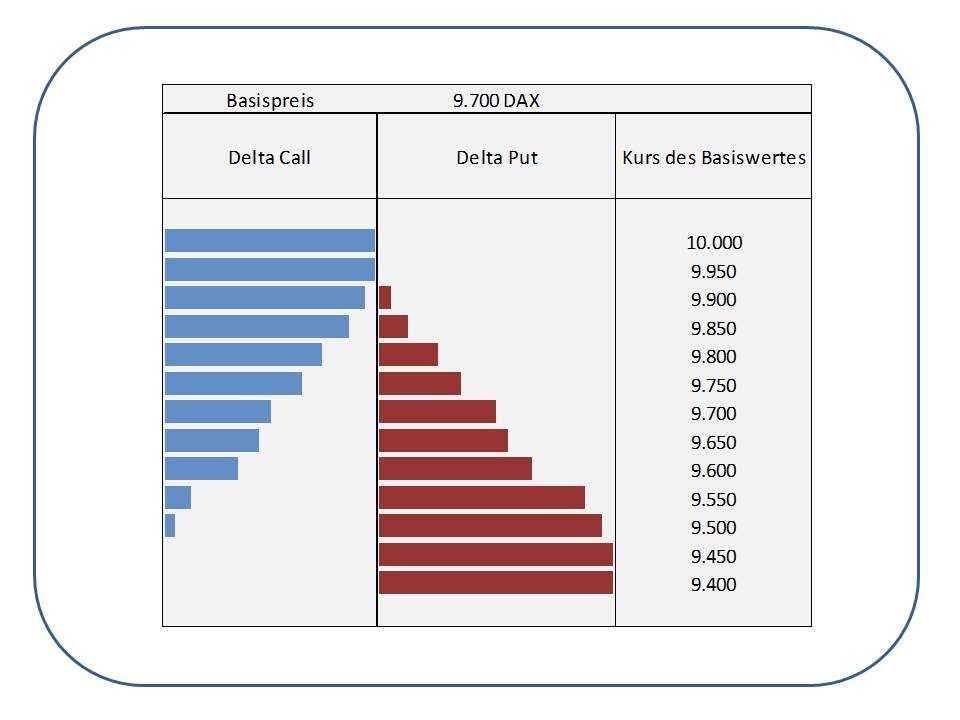
Sehen wir uns jetzt den Sachverhalt der Delta Verschiebung innerhalb eines Optionspärchens einmal schematisch in einer vereinfachten Grafik an. Hier soll es nur um die Verdeutlichung dieses Themas gehen:

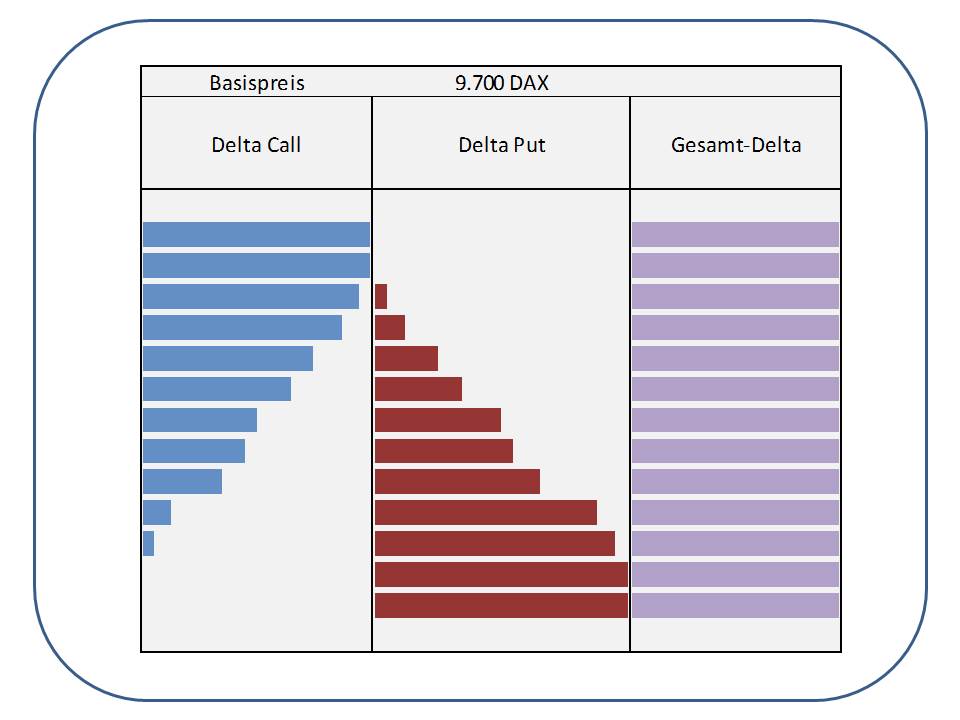
Die roten Balken ergänzen jeweils das „fehlende“ Stück des blauen Balkens, so dass die Summe aus dem blauen Balken und dem roten Balken jeweils einen Gesamtbalken darstellt, nämlich das Delta 1.

Was wollen wir jetzt aus dieser Grafik heraus lesen? Wir sehen das Hauptproblem eines Delta-Hedges einer Option gegen Basiswert, mit dem wir zu jedem Verfall konfrontiert werden und welches den Dreh- und Angelpunkt einer jeden Open-Interest-Diskussion darstellt.

Die Sicht des Market-Makers

Stellen Sie sich vor, Sie wären ein Market-Maker in Eurex-Optionen und wären verpflichtet, jederzeit für die Optionen der Basiswerte, welche Sie betreuen, handelbare Geld- und Briefkurse zu stellen. Wir bleiben der Einfachheit halber bei obigem Beispiel, nämlich Optionen auf den DAX-Index. In unserem Beispiel notiert der DAX bei 9.700 Punkten. Das heißt: sowohl der 9.700er Call, als auch der 9.700er Put haben ein Delta von jeweils 0,5.

Warum ist das so? Weil deren Ausübungswahrscheinlichkeit genau 50 Prozent beträgt. Würde der DAX zum Verfall dieser 9.700er Optionen (egal ob Call oder Put) genau bei 9.700 schließen, ergäbe sich für den Inhaber der Option keinerlei ökonomischer Nutzen, ob er nun die Option ausübt oder wertlos verfallen lässt. Er könnte den Basiswert zu 9.700 über seine Call-Option beziehen oder aber auch zu 9.700 am Markt kaufen. Der Put-Inhaber könnte den Basiswert zu 9.700 über seine Option veräußern oder auch direkt am Markt verkaufen (ebenfalls zu 9.700). Für den Verkäufer der Optionen, der Stillhalter, ist es somit bis zum Schluss nicht eindeutig klar, was der Inhaber der Option machen wird, so dass er erst nach Ausübungstermin sieht, ob er Stücke angedient oder abgenommen bekommen hat. Da dies im Vorfeld nicht hedgebar ist, findet der Optionsschreiber in einem solchen Falle am folgenden Morgen mitunter Positionsungleichgewichte in seinem Portfolio vor, welche er dann im Markt ausgleicht – deshalb haben wir nach dem Verfall von Aktien-Optionen am folgenden Handelstag zu Handelsbeginn kurze, mitunter heftige Bewegungen, welche sich immer „niemand erklären kann“. Für unser DAX-Beispiel gilt dies natürlich nicht, da es hier ein sogenanntes Cash-Settlement gibt, hier werden keine effektiven Stücke angedient oder abgenommen.

Gehen wir in unserem Beispiel weiter: jetzt werden Ihnen als Market-Maker 9.700er Calls abgekauft. Sagen wir 100 Stück. Bei einem Delta von 0,50 entspräche das einem Positions-Delta von minus 50.

Unterstellen wir jetzt, Sie würden dieses Minus sofort hedgen und wir tun jetzt so (um es zu vereinfachen), als ob ein Call oder Put bei einem vollen Delta 1 einem Future entspräche. Bei minus 50 Deltas im Optionsbuch müssten wir jetzt also 50 Futures kaufen.

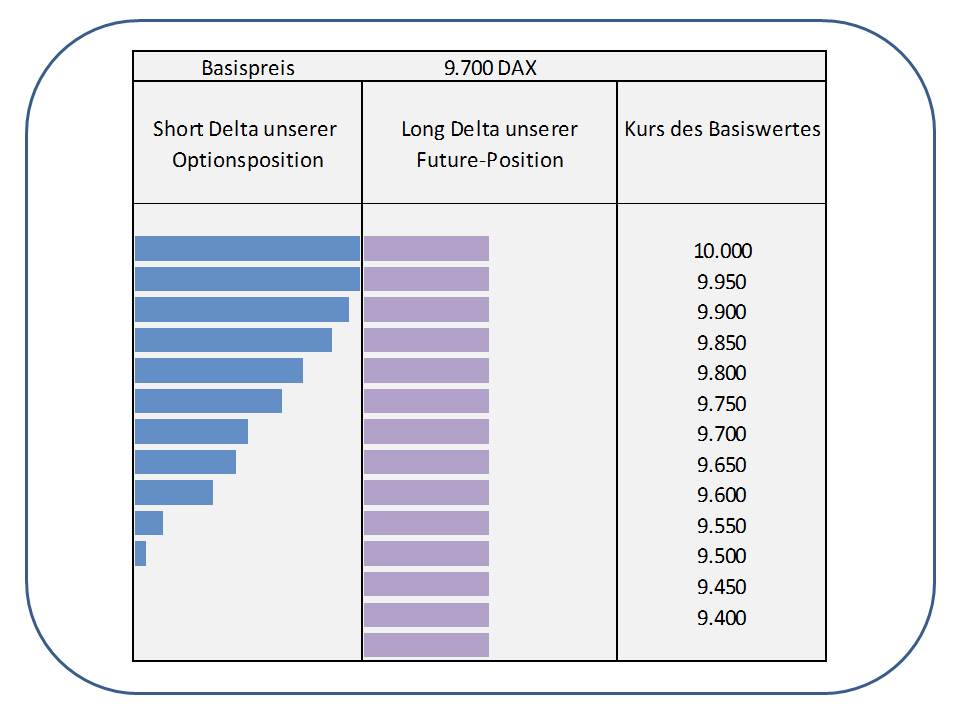
Sehen wir uns jetzt obige Grafik an, wird das Problem offensichtlich. In der Zeile des Basispreises 9.700 sind die Deltas des Calls und unserer Hedge-Position über Future gleich groß. Das heißt konkret: unsere Position ist komplett gehedged. Das Problem, welches wir mit Optionen haben ist nur leider, dass sich deren Delta verändert, wenn sich der Basiswert bewegt, während das Delta unserer Futures-Position fest verankert bleibt, da sich der Future wertmäßig linear bewegt. Steigt der Markt, wird das Delta des Calls immer größer, weil dessen Ausübungswahrscheinlichkeit ansteigt. Da Sie als Market-Maker diese Calls short sind, wird es jetzt zu einem Problem für Sie, denn Ihr Hedge läuft gegen Sie. Ihre Gesamtposition (im Delta) läuft ins Minus.

Würde der Basiswert dagegen fallen, lägen Sie ebenfalls falsch. Wie Sie obiger Grafik entnehmen können, verringert sich das Delta der Short-Calls, da deren Ausübungswahrscheinlichkeit abnimmt. Ihre Futures-Position bleibt dagegen Delta-mäßig unverändert, also werden Sie auf dem Weg nach unten immer longer.

Was macht ein „normaler Market-Maker“ im Falle, er verkauft die Calls an einen Akteur im Markt? Er kann sich die fehlende Delta-Komponente hinzuholen, nämlich über den Put. Gleicht er diese aus, kann im Anschluss im Markt passieren was will, die Gesamt-Position ist immer ausgeglichen – ohne Delta-Risiko.

Und damit haben wir jetzt das Prinzip der Optionsarbitrage erkannt – ein Prozess, welcher den deutschen Markt zu einem hohen Prozentsatz beeinflusst.

Wir sind immer noch beim Market-Maker: Wie funktioniert die Options-Arbitrage?

Wenn Call und Put über ihre Deltas immer 1 sind, heißt das doch: Call und Put bilden den Basiswert synthetisch ab. Damit ist gemeint: ich kann jede Komponente dieses Dreiergespanns, nämlich Basiswert, Call, Put aus der Kombination der zwei anderen Werte synthetisch nachbilden. Und wenn ich das kann, dann bestehen Arbitragemöglichkeiten, wenn es mir als Market-Maker gelingt, den nachzubildenden Wert billiger oder teurer darzustellen, als das Original im Markt gehandelt wird und erziele so einen risikolosen Arbitrage-Gewinn.

Ich möchte dies an einem Beispiel erklären:

Der Kauf eines Calls bringt mir ein positives Delta ins Buch. Kaufe ich z.B. 100 Calls mit einem Delta von 0,8, hätte ich 80 Deltas im Buch. Der Put des gleichen Basispreises muss ja nun ein Delta von 0,2 haben (denn in der Gesamtsumme (als natürliche Zahl betrachtet), ergeben Call und Put eines Pärchens immer ein Delta von 1). Da in der Realität die jeweilige Ausübungsrichtung das Vorzeichen der Option vorgibt, hat ein Call ein positives Delta, ein Put ein negatives Delta. Da ich also 100 Calls gekauft habe, muss ich jetzt 100 Puts gleicher Basis, gleicher Laufzeit verkaufen, was mir 20 Deltas long einbringt. Ich bin jetzt 100 Deltas long im Buch. Um mich jetzt zu hedgen verkaufe ich 100 Futures und bin Delta neutral. Egal was der Markt jetzt auch macht, egal wie sich die Deltas meiner Einzel-Optionen jetzt verändern – ich bin IMMER neutral in DIESER Position. Wenn es mir jetzt noch gelungen ist, durch den Kauf des Calls und den Verkauf des Puts den Future ein oder zwei Punkte billiger abzubilden / nachzubilden, als ich den Future zum Hedge jetzt am Markt verkaufen kann, habe ich den angestrebten Arbitrage-Gewinn in der Tasche.

Daraus ergibt sich (am Beispiel einer at the money Option):

Long Call und Short Put ergibt synthetisch Long Basiswert – durch Verkauf des Basiswertes ist die Position wieder Delta-neutral.

0,5 (long Call) + 0,5 (short Put) = 1 (synthetisch underlying long)

dagegen short underlying = -1 

Gesamtposition = Delta 0 

Short Call und Long Put ergibt synthetisch Short Basiswert – durch Kauf des Basiswertes ist die Position wieder Delta-neutral.

-0,5 (short Call) – 0,5 (long Put) = -1 (synthetisch underlying short)

dagegen long underlying = 1 

Gesamtposition = Delta 0 

-1 (short underlying) + 0,5 (short Put) = -0,5 (synthetisch Call short)

dagegen Call long = 0,5 

Gesamtposition = Delta 0 

1 (long underlying) – 0,5 (long Put) = 0,5 (synthetisch Call long)

dagegen Call short = -0,5 

Gesamtposition = Delta 0 

U.S.W.

So lässt sich jede der drei Seiten konstruieren, was im Markt einen nicht unerheblichen Umsatz produziert

Doch wie kommt nun das Open-Interest zu Stande, für welches wir uns interessieren?

Wir haben uns jetzt die Seite des Market-Makers angesehen und festgestellt, dass dieser seine Position in der Regel risikoneutral hält. Er baut zwar unter Umständen beeindruckende Positionsgrößen auf, doch sind diese meist ausgeglichen. Damit sind die Market-Maker und über diese die Banken nicht die Risikofaktoren im Markt, wie oft fälschlicherweise angenommen wird.

Das Problem entsteht, wenn kein Ausgleich gesucht wird, sondern ein Akteur bewusst eine Risiko-Position eingeht. Warum geht jemand Risiken ein? Weil er einen spekulativen Gewinn erzielen will. Der Market-Maker verdient über seine Arbitrage immer nur kleine Beträge, dafür versucht er dies aber stetig und unter ständiger Beachtung des Risikos.

Ein Optionsschreiber geht bewusst Risiken ein, mit dem Ziel, ein Vielfaches dessen zu verdienen, als ein risikoscheuer Market-Maker.

Wechseln wir jetzt die Perspektive: Sie sind jetzt ein klassischer Großinvestor (z.B. ein Fonds-Manager) und haben einen hohen Bestand xy-Aktien im Depot. Diese wollen Sie (a) nicht verkaufen, sondern halten und (b) Sie wollen monatlich ein zusätzliches Einkommen generieren. Wir unterstellen weiterhin, Sie haben 10.000 Stück dieser Aktien und wir nehmen an, diese notieren aktuell bei 100 Euro.

Jetzt fokussieren Sie sich auf den Call mit Basispreis 110 Euro und einer Restlaufzeit von etwa 30 Tagen. Der Call ist weit aus dem Geld. Dennoch kostet er noch etwas. Warum ist das so?

Der Preis einer Option setzt sich immer aus zwei Teilen zusammen: dem inneren Wert und dem Zeitwert. Der innere Wert ist real, der Zeitwert spiegelt die Wahrscheinlichkeit wider, mit der diese Option noch eine Ausübung bis oder am Verfallstag werden könnte. Je höher die Wahrscheinlichkeit (noch viel Zeit bis zum Verfall oder hohe Volatilität), desto höher der Zeitwert.

Der innere Wert errechnet sich wie folgt:

Bei einem Call: Kurs des Basiswertes – Basispreis (wobei der innere Wert niemals negativ wird, sondern bei Null verbleibt, wenn die Differenz negativ wäre).

Beispiel: Aktienkurs 110 Euro, Basispreis des Calls 100 Euro. Innerer Wert = 110 Euro – 100 Euro = 10 Euro innerer Wert

Bei einem Put: Basispreis – Kurs des Basiswertes (wobei auch hier der innere Wert niemals negativ wird, sondern bei Null verbleibt, wenn die Differenz negativ wäre).

Beispiel: Aktienkurs 90 Euro, Basispreis des Puts 100 Euro. Innerer Wert = 100 Euro – 90 Euro = 10 Euro innerer Wert

In unserem obigen Beispiel hätte jetzt also der Call einen inneren Wert von Null, da der Basispreis über dem aktuellen Kurs der Aktie liegt. Das heißt, das was er jetzt noch kostet, wäre somit die Prämie, welche sich aus der Optionsformel ergibt und über den Zeitwert die Wahrscheinlichkeitsprämie einer möglichen Ausübung widerspiegelt. Was wäre die Ausübungswahrscheinlichkeit nun konkret? Sie wäre die Wahrscheinlichkeit, dass der Basiswert (unsere Aktie) noch bis zum Verfall über den Basispreis (unsere 110 Euro) steigt.

Diesen Call suchen Sie sich als Aktien-Inhaber aus und verkaufen diesen. Nehmen wir an, der Call hätte noch einen Preis von 1,5 Euro und nehmen wir weiterhin an, Sie könnten über die nächsten 1 bis 2 Tage 10.000 Calls zu diesem Preis verkaufen (was in der Realität nicht ganz so geschmeidig ablaufen würde), hätten Sie 15.000 Euro Prämie kassiert. Ihre Strategie ist es jetzt, dass Sie darauf setzen, dass die Aktie in den nächsten 30 Tagen, nämlich bis zum Verfallstermin, nicht 10 Prozent steigt. Dann würde der Call in 30 Tagen auslaufen und der Betrag wäre Ihr realisierter Gewinn. Fast alle Fonds bessern so Monat für Monat ihren Ertrag auf, in dem sie ihre Aktien veroptionieren. Diese Form des Schreibens nennt man covered short call, da die geschriebenen Calls durch Aktien gedeckt sind. Sollte die Aktie dennoch steigen, muss der Schreiber entweder versuchen die Position nach oben zu „rollen“ oder aber er verkauft dem Käufer der Option seine Aktien zu 110 Euro über das Ziehen der Calls.

Bis hierher ist noch alles im grünen Bereich. Die Spekulationen fangen an, wenn Markterwartungen z.B. aggressiver umgesetzt werden. Stellen Sie sich vor, Sie sind positiv für die Aktie xy eingestellt. Diese notiert bei 100 Euro. Sie erwarten in den nächsten 30 Tagen einen Anstieg von bis zu 5 Prozent, an denen Sie partizipieren wollen, ohne dafür jedoch auch nur einen Cent Eigenkapital zu investieren. Wir unterstellen, der 100er Call kostet 4 Euro, der 110er noch 1,50 Euro. Jetzt könnten Sie einen Call Spread kaufen, jedoch auf eine sehr aggressive Art.

Ein normaler Call Spread würde vorsehen, Sie verkaufen der 110er Call, erzielen 1,50 Euro und investieren diese in den Kauf des 100er Calls. Da Sie 1,50 Euro durch den Verkauf des 110er Calls erzielt haben, benötigen Sie nur noch 2,50 Euro Eigenkapital für den Kauf eines 100er Calls. Ihr Risiko wäre darüber hinaus begrenzt. Sollte die Aktie nicht steigen, riskieren Sie entsprechend weniger Kapital. Die aggressivste Version wäre aber: Sie verkaufen 3 Calls mit Basispreis 110 EURO, um sich einen Call mit Basispreis 100 Euro zu kaufen und behalten obendrein noch 50 Cent Prämie über. Solange die Aktie bis zum Verfall die 110 nicht übersteigt, aber z.B. auf 105 Euro steigt, machen Sie einen schönen Gewinn ohne Einsatz eigenen Kapitals. Die Risiken, welche Sie dabei eingehen, werden oberhalb der 110 Euro aber gewaltig und der Delta / Gamma Effekt würde Ihnen den Schlaf rauben.

Und dennoch: es gibt eine Vielzahl von Optionsstrategien, mit denen man sich seine Markterwartungen versuchen kann zu versilbern. Optionen sind Instrumente, mit denen Sie für jede erwartete Situation Strategien aufbauen, ja fast „komponieren“ können. Wir werden im Teil 4 die wichtigsten Strategien mit Ihren Risiko- / Ertragsprofilen diskutieren und passende Szenarien besprechen.

Kommen wir aber noch einmal auf das Open-Interest zurück. Sehen wir uns zunächst an, wie dieses überhaupt gerechnet wird, denn da gehen die meisten Fehler in der Kommentierung in der Presse und in vielen Börsenbriefen bereits los.

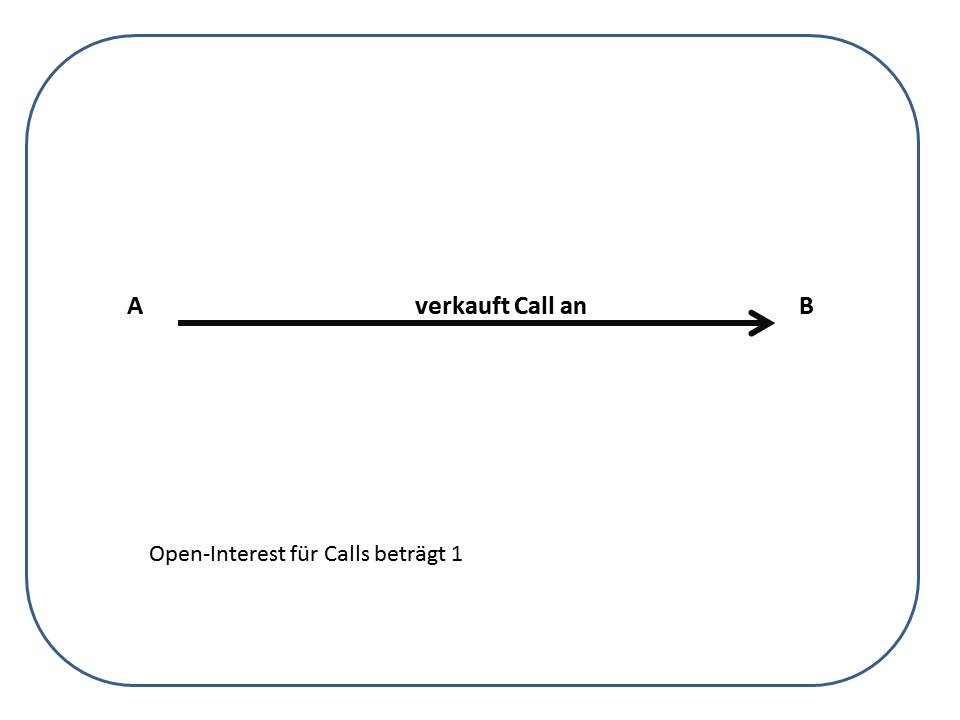
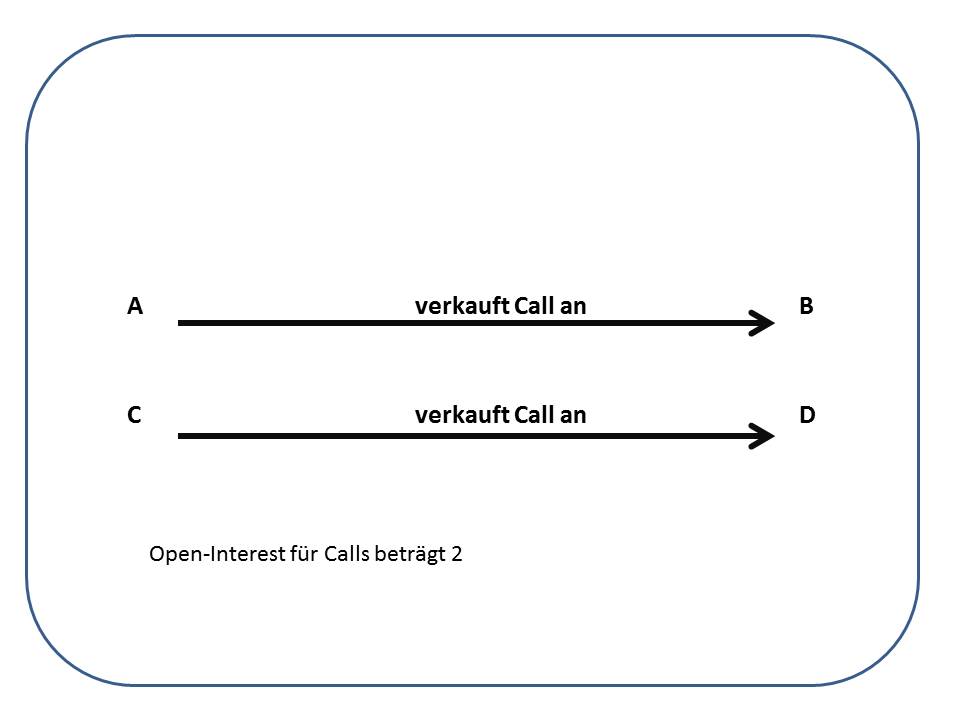
Das Open-Interest weist den Bestand offener (Options-) Positionen aus, bei Optionen unterteilt nach Calls und Puts. Stellen Sie sich vor, Herr Mayer verkauft einen Call an Herrn Müller. Jetzt haben sowohl Herr Mayer, als auch Herr Müller eine offene Position: Herr Mayer ist einen Call short, Herr Müller ist einen Call long. Im Open-Interest wird ein Wert von EINER offenen Position ausgewiesen. Jetzt verkauft Herr Schulze einen Call an Frau Bauer, wieder haben beide eine offene Position, das Open Interest erhöht sich auf ZWEI.

Frau Bauer verkauft Ihren Call nach einer Woche an Herrn Müller, der jetzt zwei Calls hält. Damit hat Herr Müller jetzt zwei Calls, Herr Mayer und Herr Schulze sind je einen Call short. Das Open-Interest beträgt noch immer einen Wert von zwei.

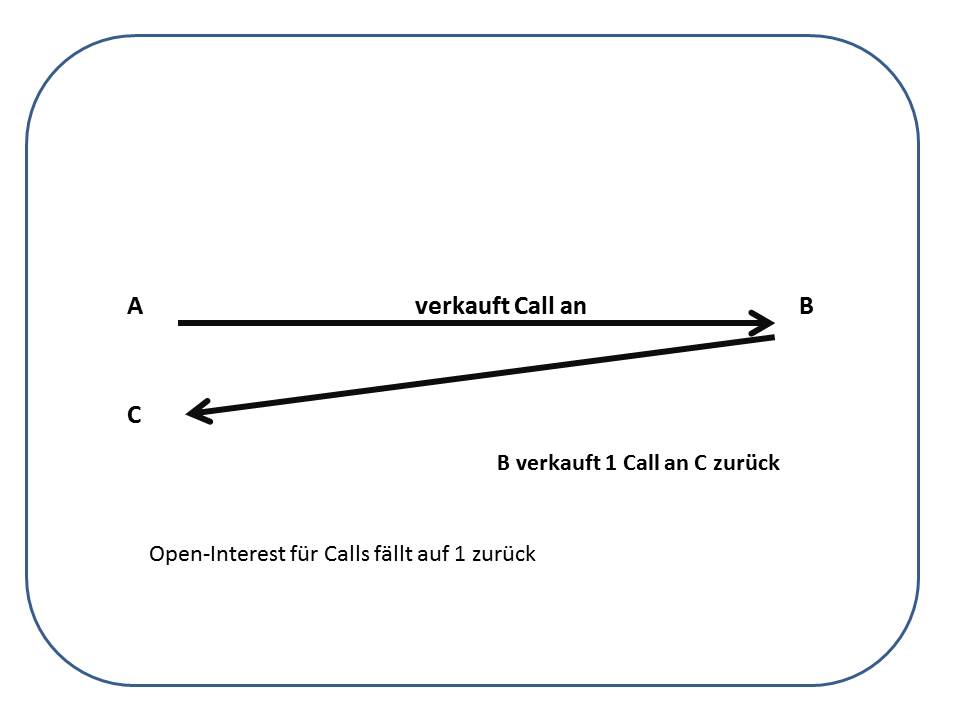
Herr Müller verkauft nun einen seiner zwei Calls und Herr Mayer kauft diesen. Damit schließen sowohl Herr Müller, als auch Herr Mayer jeweils eine Ihrer offenen Position, das Open-Interest sinkt auf eins ab.

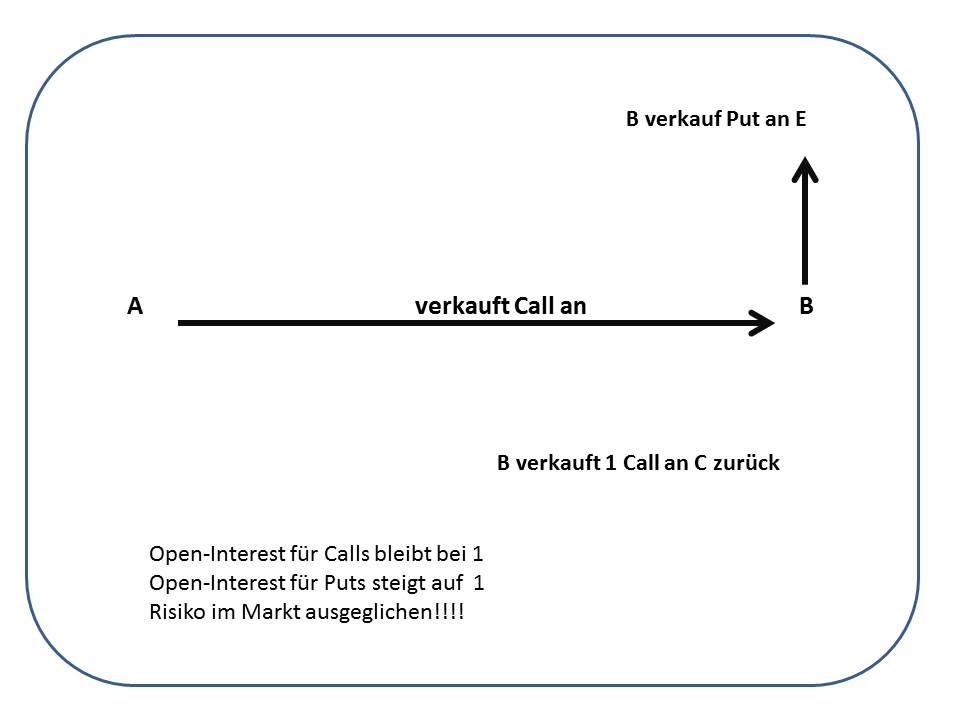
Um sein Delta-Risiko zu sichern, verkauft nun Herr Müller (der einen Call long ist) einen Put an Frau Johanna und ist damit Delta 1 in der Optionsposition und hedged dieses durch den Verkauf eines Basiswertes. Damit ist er risikoneutral, dennoch steht im Open-Interest-Ausweis auf der Call-Seite weiterhin eine offene Position. Aber auch auf der Put-Seite steht jetzt ein Open-Interest von eins.

Auf was möchte ich hinaus? Wenn wir uns immer nur eine Seite ansehen, beliebt ist die Call-Seite, sagt uns das noch gar nichts. Wir müssen auch die Put-Seite beachten. Wenn auf der Call-Seite 10.000 offene Kontrakte ausgewiesen werden, im gleichen Basispreis auf der Put-Seite aber 8.000 offene Kontrakte stehen, beträgt das echte offene Risiko nur 2.000 Kontrakte. Dieser Sachverhalt wird oft übersehen. Potentielle Probleme treten erst dann auf, wenn das Netto-Open-Interest sehr groß ist.