Grundzüge der Portfoliotheorie - Stichwort "Markowitz"

Die auf Harry M. Markowitz zurückgehende Portfoliotheorie von März 1952* ("portfolio selection theory") basiert auf der Erkenntnis, dass Investoren durch geschickt bewerkstelligte Mischungen risikobehafteter Wertpapiere (z.B. Aktien) – also durch Bildung von Portefeuilles** – ein damit verbundenes Risiko von Extremverlusten im Vergleich zu einzelnen, isoliert gehaltenen Finanzanlagen reduzieren können (Risikostreuung). Die Kernfrage der Portfoliotheorie lautet somit: Wie lässt sich das aus verschiedenen Wertpapiergattungen bestehende, optimale Portefeuille für einen Investor rational ermitteln? Mit der Beantwortung dieser Frage soll zugleich eine praktisch umsetzbare Handlungsempfehlung für eine vernünftige (objektiv situationsgerechte) Kapitalanlageplanung unter dem Risikoaspekt gegeben werden.

[* Portfolio Selection, The Journal of Finance, Vol. 7, Nr.1, März 1952]

[** Portefeuille von frz. porter, »tragen« und feuille, »Blatt«, dt.: Brieftasche; heutzutage genießt der Name "Portfolio" allgemein den Vorzug. Ein Portfolio kann als gedankliche Einheit sämtlicher Geld- und Kapitalanlagen einer Person bzw. Organisation bezeichnet werden. In diesem Sinne handelt es sich auch bei zwei oder mehreren getrennt voneinander gehaltenen Wertpapierdepots dennoch stets um ein Portfolio.]

Da Kapitalanlageentscheidungen von Investoren in der Praxis nicht selten zugleich auch eine wichtige Determinante der Finanzierungsmöglichkeiten von Unternehmungen darstellen, liegt es in der Natur der Sache, dass die Portfoliotheorie auch heute noch zu den grundlegenden Ansätzen der betriebswirtschaftlichen Investitions- und Finanzierungstheorie unter dem Risikoaspekt zählt. Fernerhin bildet sie den Ausgangspunkt für die jüngere Kapitalmarkttheorie, und dient dabei insbesondere als Fundament für ihr Kernmodell, das sog. Capital Asset Pricing Model (CAPM).

Der Leitgedanke des Verfahrens zur Portfolioauswahl, durch Investitionsmischung Unsicherheiten zu verringern, lässt sich grundsätzlich übertragen auf andere riskobeladene Handlungsmöglichkeiten jenseits der Zusammenstellung des optimalen Investitions- und Finanzierungsprogramms bei der Geldanlage in Wertpapieren: So können sich die Erkenntnisse der Portfoliotheorie beispielsweise in Industrieunternehmungen auch bei der Auswahl des besten Produktions- und Absatzprogramms unter Unsicherheit durchaus als fruchtbar erweisen.

• 2. Annahmen des Modells

Unter den vielen Möglichkeiten der Risikoerfassung greift die Portfoliotheorie auf ein Entscheidungsprinzip unter Unsicherheit zurück, das mit dem Namen μ/σ-Prinzip (Erwartungswert-Streuungsregel) in das Schrifttum eingegangen ist. Erst mit Hilfe der Annahme, dass sich das Risiko einer Investition quantitativ präzise ermittelt lässt und in der Standardabweichung (σ) der Renditen um den Erwartungswert (μ) ihrer als bekannt vorausgesetzten Renditeverteilung zu messen sei, wird eine methodische Lösung der Frage nach der optimalen Portefeuillebildung ermöglicht.

Die Anwendung der Entscheidungsregel nach den Zielgrößen Erwartungswert und Streuung (μ/σ-Prinzip) auf Portfolioentscheidungen erfordert mithin die eindeutige Charakterisierung eines jeden Wertpapiers durch zwei Parameter:

– einen "Gewinnwert", wie den Erwartungswert der Rendite μ, und

– eine Maßzahl für das "Risiko", wie die Standardabweichung σ (bzw. Varianz σ²) vom Erwartungswert μ.

Investoren bewerten somit nicht die gesamte Wahrscheinlichkeitsverteilung der möglichen Renditen eines Wertpapiers, sondern greifen stattdessen stellvertretend auf die Parameter μ und σ zurück, um so ihre Kalküle zu vereinfachen. Sollen hierbei keine Informationen aus der ursprünglichen Wahrscheinlichkeitsverteilung verloren gehen und zudem nicht gegen entscheidungstheoretische Plausibilitätsannahmen verstoßen werden, impliziert diese Vorgehensweise jedoch, dass Investitionsentscheidungen auf der Grundlage einer quadratischen Bernoulli-Nutzenfunktion und/oder auf einer bestimmten algebraischen Form der Verteilung, wie z.B. normalverteilte Renditen, zu treffen sind. Darüber hinaus beruht das Grundmodell der Portfoliotheorie auf folgenden weiteren Annahmen:

• Der Planungszeitraum beträgt genau eine Periode (T = 1), z.B. ein Jahr.

• Es werden ausschließlich monetäre Konsequenzen beachtet. Investoren verfügen über eine vorgegebene Anfangsausstattung an finanziellen Mitteln ("Budget"), welche sie im Zeitpunkt t = 0 (am Anfang der Planperiode) restlos auf eine fest vorgegebene Zahl von Wertpapieren aufteilen. Der Verkauf erfolgt im Zeitpunkt t = 1 (am Ende der Planperiode). Die Anschaffungsausgaben für Wertpapiere sind mit Sicherheit bekannt, den Einnahmen aus Dividenden und Verkaufserlösen am Ende der Periode können indes nur subjektive Wahrscheinlichkeiten zugeordnet werden. Der Erwartungswert der Rendite μ eines riskanten Wertpapiers wird damit zu einer Zufallsvariablen.

• Alle Wertpapiere sind bis in die kleinsten Quantitäten beliebig teilbar. Der Anleger kann, falls erforderlich, den Bruchteil eines Cent in jede Aktie investieren. Transaktionskosten und Steuern bleiben ausgeklammert.

• Dem Wahlverhalten der Investoren wird unterstellt, dass diese bei gleicher erwarteter Rendite diejenige Alternative mit dem geringsten Risiko vorziehen (Risikoaversion), da auch in der Realität Risikoscheu die vorherrschende Einstellung gegenüber dem Risiko zu sein scheint. Außerdem sind Investoren rational in dem Sinne, dass sie bei gleichem Risiko eine höhere erwartete Rendite weniger hohen erwarteten Renditen vorziehen (Renditemaximierung als Endvermögensmaximierung).

Angenommen, ein Investor habe sich konkrete Vorstellungen über die erwarteten Renditen und Risiken von mehreren zur Wahl stehenden riskanten Wertpapieren gemacht (was prinzipiell die Kenntnis ihrer jeweiligen Wahrscheinlichkeitsverteilung voraussetzt), und die insgesamt zur Verfügung stehende anfängliche Investitionssumme soll für diese Wertpapiere ausgegeben werden. Die Frage lautet dann: Wie soll ein risikoscheuer Investor, der seine Entscheidungen auf der Grundlage des μ/σ-Prinzips trifft, eine solche Diversifikation in optimaler Weise gestalten?

• 3. Der Lösungsansatz

Die Lösung erfolgt über einen dreistufigen Planungsansatz: Zunächst wird die Menge zulässiger Portefeuilles ermittelt ("feasible set"), sodann hieraus die Teilmenge der für jeden risikoaversen Investor effizienten Portefeuilles ausgewählt, und schließlich wird aus dieser Teilmenge das für den individuellen Anleger optimale Portefeuille bestimmt. Zulässig sind alle Portefeuilles, in denen der gesamte anzulegende Kapitalbetrag investiert ist*.

[* Werden bei der Aufteilung der finanziellen Mittel aus diesem oder jenem Grunde negative Portefeuilleanteile an einzelnen Wertpapierarten ("Leerverkäufe", "short sales") ausdrücklich zugelassen, so lassen sich diese ökonomisch als risikobehaftete Finanzierungsmöglichkeiten interpretieren.]

Die erwartete Rendite eines Portefeuilles μp entspricht hierbei der mit ihrem Anteil am Portefeuille gewichteten Summe der erwarteten Renditen der einzelnen in ihm enthaltenen Wertpapiere:

μp = ∑ xi μi , mit i = 1 .... n, wobei gilt: ∑ xi = 1 bzw. 100%.

Die einzelnen Variablen sind wie folgt bezeichnet: ∑ : Summensymbol; i: Aktie i, mit i = 1 ... n im n-Aktien-Fall; xi: prozentualer Anteil des Ausgangsbudgets, der in Aktie i investiert wird, und μi: erwartete Rendite der Aktie i.

Für das Portefeuillerisiko, gemessen in der Portfolio-Standardabweichung σp, gilt: Das Risiko eines Portefeuilles σp ist abhängig von den Varianzen der Renditen der einzelnen zu mischenden Wertpapiere (auch als Dispersion oder Streuung bezeichnet), ihren Kovarianzen (bzw. den Korrelationen; Korrelationen von +1 und –1 werden indes für alle Wertpapiere ausgeschlossen) und den Anteilen, mit denen einzelne Wertpapiere im Portefeuille vertreten sind:

σp = [∑ xi² σi² + ∑ ∑ xi xj σij]½ .

Die Summierung läuft im n-Aktien-Fall jeweils von i bzw. j = 1 .... n, wobei gilt: i ≠ j. Die Kovarianz der Renditen der Aktie i und der Aktie j ist hier durch σij symbolisiert. Dieser Ausdruck lässt sich alternativ auch wie folgt schreiben:

σp = [∑ ∑ xi xj σij]½ , wobei die Summierung wiederum über alle erfassten n Aktien läuft.

Da aus unterschiedlichsten Ursachen Verlustgefahren drohen und weil sich gegebene ökonomische Unsicherheitsursachen nicht auf alle Wertpapiere vollkommen gleich auswirken, ist das Portefeuille-Risiko auch nicht einfach nur eine Addition seiner Einzelrisiken. Entspräche das Risiko eines Portefeuilles generell seinem Durchschnittsrisiko, wäre eine Portefeuillebildung für risikoscheue Investoren eine wenig interessante Sache. Alle finanziellen Mittel wären in die Aktie mit der höchsten erwarteten Rendite im Verhältnis zu ihrem Risiko zu investieren.

Sind die einzelnen Renditen der ein Portefeuille konstituierenden Aktien indes voneinander stochastisch unabhängig, so folgt daraus immer dann eine spürbare Reduzierung des Gesamtrisikos, wenn die Anzahl der im Portfolio enthaltenen Aktien nur hinreichend groß ausfällt. Die Gefahr, dass bei allen Vermögenswerten eine negative Entwicklung gleichzeitig eintritt (einschl. eines Totalverlustes), wird hierdurch merklich reduziert. Das über Streuung erzeugte Portfolio geht sonach mit einem geringeren konsolidierten Risiko einher als die Summe der Einzelrisiken insgesamt ausmacht. Damit ist das Risiko eines Portefeuilles außer im Extremfall vollkommen positiver Korrelation zwischen den Renditen stets kleiner als das mit den Portefeuille-Anteilen gewogene Mittel der Standardabweichungen der einzelnen Wertpapiere im Portefeuille. Dieser sogenannte Diversifikationseffekt wird im Falle negativer Korrelationen zwischen den Wertpapierarten nochmals verstärkt. Unter Risikoaversion besteht die Aufgabe bei einer Diversifikation von Anlagemitteln im Hinblick auf die angestrebte Zielsetzung einer Risikoreduktion folglich darin, Mischungen von Wertpapieren mit möglichst niedrigen Korrelationen zu finden, und nicht etwa darin, eine Auswahl von Aktien zusammenzustellen, die jede für sich ein möglichst geringes Einzelrisiko aufweist.

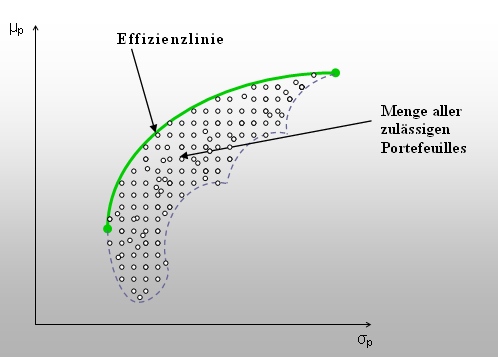
Um diese Zusammenhänge anschaulich zu machen, wird üblicherweise jedes einzelne zulässige Portefeuille durch einen einzigen Punkt in einem μ/σ-Diagramm abgebildet, indem z.B. der Risikowert σ an der Abszisse und der Gewinnwert μ an der Ordinate abgetragen wird. In einem sich anschließenden Schritt werden die vorliegenden Portefeuilles dann aufgeteilt in effiziente und ineffiziente Portefeuilles.

Abbildung: Portfoliolinie, effiziente Portfolios (grüner Linienabschnitt) und ineffiziente Portfolios

Ein Portefeuille heißt effizient, wenn es kein anderes Portefeuille gibt, das entweder bei gleichem σp ein höheres μp oder bei gleichem μp ein niedrigeres σp aufweist (bzw. ein höheres μp bei niedrigerem σp aufweist). Effizient ist somit ein Portefeuille dann, wenn kein anderes zulässiges Portefeuille existiert, das nach dem μ/σ-Prinzip eindeutig besser (dominant) ist. Man erhält die Menge an effizienten Portefeuilles, indem man die das Risiko minimierenden Anteile der zu mischenden Wertpapiere am Gesamtportfolio für alle in Frage kommenden Renditeerwartungen errechnet. Hierzu sind entsprechende mathematische Aufgaben der quadratischen Programmierung zu lösen*. Die durch Minimierung der Zielfunktion gefundenen Portefeuilles liegen dargestellt in einem μ/σ-Diagramm alle auf einer "guten" Kurve der Investitionsgelegenheiten: der sogenannten Effizienzlinie ("efficient frontier").

[* Um hier nicht in Formalismen zu den rechentechnischen Fragen einer mathematischen Optimumsbestimmung steckenzubleiben, sei zu den formalen Modellierungen auf die zahlreiche einschlägige Literatur verwiesen.]

Die Bedeutung der Effizienzlinie liegt darin, dass zur Auswahl des optimalen Portefeuilles all jene Portefeuilles, die nicht auf dieser Isoquante liegen, sich sofort ausschließen lassen, wodurch die endgültige Auswahl beträchtlich erleichtert wird.

Übertragen auf den praktischen Anwendungsfall heißt dies: Zwar trifft jeder Investor seine Anlagedisposition auf der Grundlage des Modells der Portfolioauswahl, doch rücksichtlich der persönlichen Einstellung gegenüber dem Risiko wird jeder Einzeln hierbei unterschiedlich hohe Geldbeträge auf die unterschiedlichen Investitionsmöglichkeiten verteilen. Damit liegt zugleich die Endauswahl fest, welche Aktien mit welchem Gewicht im Portfolio vertreten sind.

Der individuelle Grad der Risikoscheu der Investoren schlägt sich im μ/σ-Diagramm in einem unterschiedlichen Verlauf einer sog. Indifferenzkurvenschar nieder. Als Indifferenzkurve bezeichnet man Kombinationen von μ und σ, die den gleichen Risiko-Nutzen stiften. Bei gegebener individueller Risikopräferenzfunktion erfährt das optimale Portefeuille unter den gesetzten Modellannahmen letztlich vom Berührungspunkt der Indifferenzkurvenschar mit der Effizienzlinie seine Bestimmung.

• 4. Erweiterung des Modells um eine sichere Anlagemöglichkeit

Sobald sich Anlegern aber zusätzlich eine sichere Anlage- und Verschuldungsmöglichkeit darbietet, zu der diese im Modell Mittel unbeschränkt anlegen und aufnehmen können ("pure rate"), ist die Bildung von Portefeuilles aus risikobehafteten Investitionsobjekten keine reine Geschmackssache mehr, wenn der Investor nicht gegen Rationalitätsannahmen verstoßen will. Das einzige Portefeuille, das jetzt die Existenz dominanter Positionen ausschließt, ist das Tangentialportefeuille auf der von Sicherheitszins ausgehenden Tangente an die Effizienzlinie der riskanten Wertpapiere im μ/σ-Diagramm. Alle nicht dominierten (und daher effizienten) Portefeuilles liegen auf dieser Tangente. Das bedeutet aber: Jede effiziente Mischung ist eine Kombination des Tangentialportefeuilles mit der sicheren Anlage- und Verschuldungsmöglichkeit. Die Struktur des in jeder effizienten Mischung beschlossenen Portefeuilles riskanter Wertpapier ist somit immer die gleiche; sie ist insbesondere unabhängig davon, welche Position ein Investor nach seinen individuellen Verhältnissen letztlich auf der Effizienzgeraden im μ/σ-Diagramm einzunehmen plant und damit in letzter Linie auch unabhängig vom Grad der Risikoaversion (Tobin-Separation*). Je nach Ausmaß seiner Risikoscheu wird der Investor in einem nächsten Schritt das zuvor ermittelte Portefeuille mit mehr oder weniger Anlage zum Sicherheitszinssatz verbinden, bei geringer Risikoscheu aber auch mit Verschuldung zum Sicherheitszinssatz. Man bezeichnet dieses modelltheoretische Ergebnis deswegen als "Separationstheorem", weil sich das Entscheidungsproblem zur optimalen Wertpapiermischung prinzipiell in zwei Phasen trennen lässt:

1. Die Bestimmung der Zusammensetzung des optimalen Portefeuilles, welches unabhängig vom Ausmaß der Risikoaversion des Investors ist, und

2. die Kombination dieses Portefeuilles mit sicherer Anlage oder Verschuldung unter Beachtung der persönlichen Risikoeinstellung.

[* James Tobin wurde 1981 mit dem Nobelpreis für Wirtschaftswissenschaften ("Wirtschaftspreis") ausgezeichnet.]

• 5. Kritisch Würdigung der Portfoliotheorie

Die normative Portfoliotheorie liefert Antworten auf die Fragestellung, wie sich risikoscheue Investoren, die nach Erwartungswert und Streuung entscheiden (d.h. sich am μ/σ-Prinzip orientieren), vernünftig verhalten können. Sie macht dabei deutlich, dass sich durch Mischung von Investitionsobjekten Risiken vernichten lassen. Neben der Problematik aus entscheidungstheoretischer Sicht ist die Anwendung des μ/σ-Prinzips auf reale Entscheidungssituationen jedoch aus folgenden Gründen nur begrenzt möglich:

1. Ein großes Problem bei der Anwendung des Modells ist in der Informationsbeanspruchung zu sehen: Zur Berechnung benötigt man für alle Objekte nicht nur die Erwartungswerte und Standardabweichungen der zukünftigen Einzahlungen, sondern auch alle Kovarianzen; bei n Objekten gibt es allein n × (n – 1) / 2 Kovarianzen. Mag es bei Wertpapieren durchaus möglich sein, die erforderlichen Daten auf der Grundlage statistischer Berechnungen abzuschätzen, so stößt ihre Ermittlung bei Sachinvestitionen auf schier unlösbare Probleme.

2. Der Planungszeitraum bezieht sich auf lediglich eine Periode. Investitionen wirken sich aber i. Allg. über mehrere Perioden aus. Die Erweiterung des Modells auf mehr als zwei Zahlungszeitpunkte würde aber eine erhebliche Komplizierung bedeuten, außerdem ein Ansteigen des ohnehin schon großen Datenbedarfs.

3. Das μ/σ-Prinzip setzt eine quadratische Risikonutzenfunktion der Anleger und/oder eine bestimmte Form der Wahrscheinlichkeitsverteilung, z.B. eine Normalverteilung der Renditen sämtlicher Wertpapiere voraus. Empirische Untersuchungen hingegen deuten bei riskanten Wertpapieren eher hin auf Verteilungen mit unendlicher Varianz bei höheren Dichten, insbesondere für mittlere sowie sehr hohe und sehr niedrige Renditen. Zudem erscheinen quadratische Nutzenfunktionen empirisch äußerst fragwürdig; quadratische Nutzenfunktionen haben nämlich die erfahrungswissenschaftlich zweifelhafte Eigenschaft zunehmender Risikoaversion bei steigenden Renditeerwartungen.

4. Das Separationstheorem wird im Falle der Sachinvestitionsplanung kaum gelten, weil hier beliebige Teilbarkeit noch weniger vorausgesetzt werden kann als bei Wertpapieren.

Auch wenn das Modell zur Portfolioauswahl aufgrund dieser überaus engen Anwendungsvoraussetzungen für den praktischen Einsatz zunächst wenig geeignet erscheint, führt es doch die wesentlichen Zusammenhänge deutlich vor Augen: So wird die Bedeutung der in den Kovarianzen zum Ausdruck kommenden stochastischen Abhängigkeiten (Interdependenzen) zwischen den Investitionsobjekten erkennbar: Bei der Beurteilung von Einzelprojekten ist das durch die Standardabweichung gemessene Gesamtrisiko nicht ausschlaggebend, da ein Teil dieses Risikos (namentlich das "unsystematische Risiko", d.h. das Aktien inhärente branchen- bzw. unternehmensspezifische Risiko, welches bei isolierter Betrachtung regelmäßig überwiegt) durch effiziente Mischung mit anderen Objekten vermieden werden kann.

Wichtig ist das verbleibende Restrisiko: das sog. "systematische Risiko", das auch als gesamtwirtschaftliches Risiko oder Markt-Risiko bezeichnet wird, und durch Diversifikation nicht eliminiert werden kann (sich wohl aber durch Hedging gezielt kompensatorisch steuern lässt). Nur dieser Teil des Gesamtrisikos eines untersuchten Investitionsobjekts liefert den maßgeblichen Beitrag zum Risiko des gesamten Investitionsprogramms. Das systematische Risiko wird durch die Kovarianz bzw. das Verhältnis von Kovarianz zur Varianz des Gesamtprogramms erfasst. Das letztere (relativierte) Risikomaß heißt Beta (β) und spielt in der neueren Kapitalmarktgleichgewichts- und Finanzierungstheorie, insbesondere im Modell der Wertpapierlinie (CAPM), im Marktmodell (MM) und der Arbitrage Pricing Theory (APT), eine herausragende Rolle.

Ziel des CAPM, welches auf der Portfoliotheorie fußt, ist es, Konkurrenzgleichgewichtspreise für Wertpapiere unter Ungewissheit herzuleiten. Nach dem CAPM ist die erwartete Rendite einer Aktie im hierbei vorausgesetzten Kapitalmarktgleichgewicht eine lineare Funktion der durch ihr β gemessenen Risikomenge. Wie bereits ausgeführt, ist der β-Faktor eines individuellen Wertpapiers definiert als der Quotient aus Kovarianz des betreffenden Wertpapiers zur Varianz des Marktportefeuilles. Vereinfacht behauptet das CAPM: Der Erwartungswert der Rendite einer risikobehafteten Anlagemöglichkeit (z.B. Aktie) setzt sich im Marktgleichgewicht zusammen aus dem risikolosen Geldmarktzinssatz plus einer Risikoprämie. Die Risikoprämie ist das Produkt aus dem Marktpreis für das Risiko (= Differenz zwischen Erwartungswert der Rendite des Markt-Portfolios und der sicheren Anlagemöglichkeit) mit der marktrelevanten Risikomenge der risikobehafteten Anlagemöglichkeit β. Die Anwendung von β im Rahmen der "asset allocation" setzt aber voraus, dass auch das μ/σ–Prinzip praktisch angewandt werden kann. Die Vielzahl an argen Modellvereinfachungen entleert hier offensichtlich den Anspruch, das CAPM könne die Börsenkurse in der Realität adäquat erklären.

Als wesentliches Ergebnis dieser Überlegungen bleibt festzuhalten, dass Investitions- und Finanzierungsentscheidungen auf der Grundlage des μ/σ-Prinzips immer nur im Kontext eines diversifizierten Portfolios Sinn ergeben. Die Beurteilung der Vorteilhaftigkeit einzelner Kapitalanlagen wird der Disponierende folglich nicht losgelöst von der Struktur der übrigen risikotragenden Anlagemöglichkeiten, sondern "simultan" zu treffen haben. Das relevante Risikomaß für einzelne Anlageobjekte im Rahmen eines vollständig diversifizierten Portefeuilles ist hierbei ausschließlich das Kovarianzrisiko.

Harry M. Markowitz, amerikanischer Wirtschaftswissenschaftler, *Chicago 24. 08. 1927; Professor an der City University of New York und Begründer der Portfolio-Selection Theory; Harry M. Markowitz erhielt 1990 zusammen mit Merton Howard Miller und William F. Sharpe für seine bahnbrechenden Forschungen zur betrieblichen Finanzmarkt- und Finanzierungstheorie den Nobelpreis für Wirtschaftswissenschaften ("Wirtschaftspreis").

Autor: Bert H. Deiters

"Das 1x1 des Futurestrading" aus dem Wissensbereich von GodmodeTrader.de :

http://www.godmode-trader.de/wissen/futures/

World of Trading 2024: Triff die stock3-Experten live vor Ort

Am 22. & 23.11. findet die World of Trading in Frankfurt statt & stock3 ist mit dabei. Wir laden Dich ein, uns & unsere Experten näher kennenzulernen. Mit dabei sind u.a. Bastian Galuschka, Sascha Gebhard u.v.m.

Jetzt kostenloses Ticket sichern!