Fibonacci-Analyse und Fibonacci-Trading: Die Know-how-Serie!

Diesen Stein brachten Anfang des 20. Jahrhunderts zwei US-Charttechniklegenden ins Rollen: Ralph Nelson Elliott (1871 – 1948), dem wir die nach ihm benannte Elliott-Wellen-Theorie verdanken, und parallel dazu der legendäre Trader William Delbert Gann (1878 – 1955), der die nach ihm benannte Ganntheorie entwickelte.1 

Mittlerweile gibt es kaum eine Chartsoftware, die nicht mit Fibonacci-Retracements,- Extensionen, -Fächern oder -Zeitprojektionen angeboten wird. Und dennoch gibt es bei der Anwendung und der Umsetzung ins Trading viele Fragen oder Missverständnisse, die dazu führen, dass das volle Potenzial der Methode nicht ausgenutzt wird.

Daher will ich sowohl der Frage nachgehen, warum und auf welche Weise Fibonacci-Analysen treffsicher und risikominimierend eingesetzt werden können als auch warum die immanente Logik der Fibonacci-Regeln an den Weltbörsen zum Tragen kommt.

Grundsätzlich muss festgehalten werden, dass Börsenhandel immer mit Entscheidungen unter Unsicherheit einhergeht. Die Märkte sind komplex, d.h. der weitere Verlauf kann zwar in einem Wahrscheinlichkeitsrahmen eingegrenzt, jedoch nicht en détail geplant oder vorausberechnet werden. Niemand hat eine Glaskugel und niemand den 100 %-Trade. Dennoch werden Sie erkennen, dass man mit der Fibonacci-Methode diese Unsicherheiten auf ein erträgliches Maß reduzieren kann.

Fibonacci ist deshalb so hilfreich, weil es sich um eine Vermessung des Kursverlaufes handelt, die mathematisch abgeleitete, relative Niveaus ermittelt, die für die Zukunft entscheidende Handelsmarken darstellen. Entscheidend in zweierlei Hinsicht:

Zum einen werden Marken aufgespürt, an denen eine signifikante Kursreaktion zu erwarten ist. Prinzipiell kann es sich dabei um die Bedingungen bzw. das Signal für die Fortsetzung eines Trends, den Übergang in eine Seitwärtsphase oder den Start einer entgegengesetzten Trendbewegung handeln. Daher können sie auch verwendet werden, um die Ergebnisse anderer technischer Setups zu bestätigen (z.B. Chartformationen, Candlestickmuster, Indikatorensignale, etc.). Ist der Kursverlauf einmal mittels Fibonacci-Verhältnissen vermessen, können Bewegungen zueinander in Beziehung gesetzt, das Potenzial eines Trends mit entsprechenden Kurszielen abgeschätzt, künftige Widerstands- und Unterstützungsmarken erfasst und Rückschlüsse über den weiteren Verlauf gezogen werden.

Zum anderen lassen sich Bedingungen aufstellen, welches Verhalten der Kurs zeigen muss, damit die eigenen Vorannahmen oder die Art des bisherigen Trendverlaufs bestätigt werden. Im Sinne einer „wenn- dann“ - Analyse kann der Kursverlauf von vorne herein auf sein künftiges Potenzial abgeklopft und weitere Entwicklungsvarianten schon in ihrer Entstehungsphase mit in die Überlegungen eingebaut werden.

Ein weiterer zentraler Vorteil der Fibonacci-Analyse liegt in der großen Flexibilität und Vielseitigkeit. Man kann die Werkzeuge für jeden Basiswert und unabhängig vom aktuellen Trend, dem zugrunde liegenden Markt, der gehandelten Zeitebene oder dem individuellen Anlagehorizont einsetzen.

Vereinfacht gesagt teilt die Methode aktuelle Trendphasen und den künftigen Kursverlauf in tradenswerte und neutrale Phasen. Diese Segmentierung reduziert das Risiko des verfrühten Ein- oder Ausstiegs bei laufenden und geplanten Investments, ermöglicht die Umsetzung passgenauer Tradingpläne, liefert exaktere Stopps und schließlich mehr Interpretationskompetenz über den potenziellen künftigen Verlauf des gehandelten Marktes. Mit der entsprechenden Übung kann man konstruktiv und gelassen mit den zuvor vermeintlich chaotischen Kurswechseln umgehen und wahrscheinlichkeitsbasierte Fahrpläne für den Markt und die Trades erstellen.

Daher ist es für jeden Anleger - egal ob Aktiensparer oder Daytrader - unverzichtbar, sich mit den Grundlagen und Vorzügen der Fibonacci-Methode auseinanderzusetzen.

Fibonacci-Zahlenreihe

Um mit der Komplexität, den schnellen Wechseln, den rasanten Anstiegen, scharfen Einbrüchen oder zermürbenden Seitwärtsphasen der Märkte und den daraus resultierenden Problemen und Unsicherheiten als Trader oder Investor umgehen zu können, braucht es ein Instrument, das sich genau auf diese Zusammenhänge und Phänomene versteht. Und fündig werden wir dabei bei einem Mathematiker aus der Toskana, den vor 900 Jahren seine Beobachtungen über Kaninchen berühmt gemacht haben.

Mehr als 1.000 Jahre nachdem die Griechen die Mathematik in Europa bereits zu enormer Blüte geführt hatten, wurde Leonardo von Pisa 1175 n. Chr. geboren und sollte als erster bedeutender Mathematiker in die Europäische Geschichte nach Christi Geburt eingehen. Inspiriert von der indisch-arabischen Zahlenlehre, die er auf vielen Reisen nach Griechenland, Algerien und Ägypten kennenlernte, schrieb er in seinem Werk „Liber Abaci“ von 1202 eine umfassende Abhandlung über die arabische Arithmetik und ergänzte dieses in Europa unbekannte Wissen mit seinen eigenen Überlegungen. Leonardo von Pisa war ein exzellenter Beobachter der Natur und hat seine Formeln aus diesen Erkenntnissen abgeleitet. Die Fibonacci-Zahlenreihe – also die Basis für weitere Berechnungen, die auch in der Charttechnik Verwendung finden - entdeckte er in einem sprichwörtlichen „Feldversuch“:

Eine seiner Berechnungen ging der Frage nach, wie man die Entwicklung von Populationen hochrechnen kann. Er verwendete dafür das Beispiel der Vermehrung von Kaninchenpaaren innerhalb eines Jahres.

Ausgangspunkt dieses mathematischen Modells sind Kaninchen, die einen Monat bis zur Geschlechtsreife benötigen und anschließend Monat für Monat ein neues Paar in die Welt setzen. Diese „mathematischen Kaninchenpaare“ sind zudem der Einfachheit halber für den Messzeitraum unsterblich und pro Paar in ein Männchen und ein Weibchen aufgeteilt.

Gestartet wird das Modell in Monat 1 (Januar) mit einem Paar, das einen Monat benötigt um geschlechtsreif zu werden. Im März wirft das Paar ein weiteres Paar. Dieses benötigt nun einen Monat, um seinerseits geschlechtsreif zu werden, während das Ursprungspaar im vierten Monat ein weiteres Paar zur Welt bringt. Damit befinden sich nach vier Monaten drei Kaninchenpaare im Gehege. Im Mai wird das dritte Paar geschlechtsreif und Paar 1 und Paar 2 bekommen wiederum Nachkommen. Damit haben wir neben den drei alten Paaren zwei neue im Gehege. In der Summe sind dies schon fünf Paare nach fünf Monaten. Nach sechs Monaten sind es bereits acht Paare und zu Ende des Jahres 144 Paare. Spätestens zu diesem Zeitpunkt sollte das Gehege vergrößert werden.

Bei der mathematischen Struktur, die dieser Entwicklung zugrunde liegt und die es im Endeffekt ermöglicht, das Wachstum der modellhaften Kaninchenpopulation auch für drei, sieben oder 20 Jahre hochzurechnen, handelt es sich um eine bahnbrechende Erkenntnis. Denn sie beschreibt mathematisch die Haupteigenschaften von Wachstumsprozessen, die auch für andere Bereiche in der Natur verallgemeinert werden können:

Jede neu auftretende Anzahl an Paaren ist die Summe der beiden vorangegangenen.

Zu Beginn gibt es ein Paar, das nach einem weiteren Monat geschlechtsreif wird, gefolgt von zwei Paaren nach drei Monaten, (2+1) = 3 Paaren nach vier Monaten, (3+2) = 5 Paare nach fünf Monaten, (5+3) = 8 Paare nach sechs Monaten, anschließend 13, 21, 34, 55, 89, 144, 233 und so fort. Es entwickelt sich eine exponentiell wachsende Population, bei der jeder neue Generationszyklus um die Anzahl der vorherigen Kaninchenpaare größer ist, als der vorherige Zyklus.

Mathematisch lautet die entsprechende Formel:

fn = fn-1 + fn-2 für n > 2 

Damit ergibt sich die unendliche Fibonacci-Zahlenreihe, die mit der Zahl 1 beginnt und bei der jeder Term (ausgenommen die ersten beiden) durch Addition von zwei direkt aufeinander folgenden Termen gebildet wird:

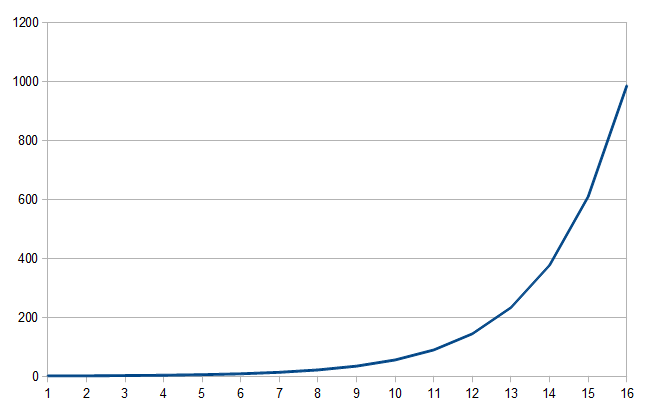
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 

Abb. 1: Kurve der ersten 16 Fibonacci-Zahlen; Y-Achse: Wert der Fibonacci-Zahl (1,1,2,3,5,...); Y-Achse: Rangnummer der Zahl

Etwas philosophischer könnte man das Ergebnis so formulieren: Innerhalb von Entwicklungs- oder Wachstumsprozessen (und nichts anderes sind Fibonaccis fruchtbare Kaninchen) ist die Gegenwart, der aktuelle Status Quo der Entwicklung, immer die Summe der vergangenen Entwicklungen. Und die Zahlenreihe liefert hierfür den mathematischen Beweis.

Das Besondere ist die Tatsache, dass die Sprünge bzw. die Zuwächse zwischen den einzelnen Zahlen einem bestimmten Muster des organischen Wachstums oder der Ausdehnung folgen. Diese harmonischen Verhältnisse finden sich in zahllosen Beispielen in der Natur, wo sie Ergebnis eines Jahrmillionen dauernden Entwicklungs- und Optimierungsprozesses sind. Denn die Ursache für das Auftreten der Fibonacci-Zahlen in der DNA dieser und vieler anderer Beispiele ist, dass es sich häufig um die effektivste Form der Ausrichtung, der Anordnung, des Wachstums oder der Entwicklung handelt.

Mathematisch betrachtet ist dabei jedoch nicht nur die Folge an sich interessant, sondern insbesondere die Verhältnisse der Zahlen zueinander.

Betrachtet man die Zuwachsrate von einer Fibonacci-Zahl zur nächsthöheren, fällt auf, dass sich diese relativ rasch dem Wert 1,618  annähert (z.b. 89 * 1,618 = 144,002). Dieser Faktor kann nicht nur zur Berechnung einer jeweils folgenden Fibonacci-Zahl verwendet werden. Er beschreibt letztlich die Veränderungsrate aller Fibonacci-Zahlen zur jeweils folgenden und damit das gesamte System. Dies sollte den europäischen Gelehrten nicht lange verborgen bleiben:

Als der Mathematiker und Astronom Johannes Kepler (1571 – 1630) vor rund 400 Jahren seine Gesetze der Planetenbewegungen entwickelte, fiel ihm nicht nur dieser Zusammenhang auf, sondern auch, dass sich damit die Verhältnisse zweier aufeinanderfolgender Fibonacci-Zahlen der irrationalen Zahl Phi (Φ) annäherten. Zuvor hatte er bereits den Zusammenhang zwischen den Fibonacci-Verhältnissen und dem Goldenen Schnitt entdeckt.

Der von Euklid (365 – 300 v. Chr.) erstmals mathematisch beschriebene Goldene Schnitt besagt, dass eine Strecke so in zwei Teilstrecken geteilt wird, dass das Verhältnis der kurzen zur langen Teilstrecke dasselbe ist, wie das Verhältnis der langen Teilstrecke zur Gesamtstrecke. Das „göttliche Verhältnis“, wie es rund 1.500 Jahre später bei den christlichen Mönchen und in Kunst und Architektur heißen sollte, war „geboren“.

Der goldene Schnitt ist jedoch nichts anderes, als die Aufteilung einer Strecke mittels der Zahl Φ in ein kurzes und ein um Φ (1,618033..)-mal längeres Teilstück. Fibonacci-Verhältnisse nähern sich dieser „goldenen“ Zahl an, indem man eine Fibonacci-Zahl durch ihren Vorgänger dividiert. Je höher das Zahlenpaar dabei auf der Skala angesiedelt ist, umso exakter nähert sich dessen Divisionsergebnis der Zahl Φ an. Damit lässt sich jede höhere Zahl der Fibonacci-Folge mit fn = Φ * fn-1 beschreiben.

Ein weiteres, zentrales Fibonacci-Verhältnis, lässt sich mit Φ darstellen und zeigt eine erstaunliche Eigenschaft der Zahl: Der Kehrwert von Φ ist die Verhältniszahl 0,618033 .. und hat exakt die gleichen Nachkommastellen wie die Zahl Φ. Eine Eigenschaft, die außer Φ keine andere Zahl besitzt.

Alle weiteren relevanten Verhältniszahlen weisen dieselben Annäherungsergebnisse, wie die auf Φ basierende „goldene Zahlenfolge“ auf. Diese hat die Eigenschaft, dass drei aufeinanderfolgende berechnete Zahlen immer im Verhältnis eines goldenen Schnittes zueinander stehen. Ausgehend von Φ folgen für Φ² = 2,618, Φ³ = 4,236 oder z.b. Φ-1 = 0,618, Φ-2 = 0,382 und Φ-3 = 0,236 weitere typische Fibonacci-Zahlenverhältnisse.

Zusammenfassend lässt sich sagen, dass die Zahl Φ, deren Eigenschaften Euklid entdeckte, und die damit eng verbundene Fibonacci-Zahlenreihe, die Leonardo von Pisa in die europäische Mathematik eingeführt hat, bei Kepler, Gaus, Moivre und Binet, bis hin zu den Fraktalen eines Benoît Mandelbrot in der Mathematik eine enorme Rolle spielen.

Auf welche Weise diese im Börsenhandel relevant werden, betrachten wir in den folgenden Artikeln.