Capital Asset Pricing Model (CAPM)

Das Capital Asset Pricing Model (CAPM, Modell der Wertpapierlinie) wurde von William F. Sharpe, John Lintner und Jan Mossin in den 60er Jahren des letzten Jahrhunderts unabhängig voneinander entwickelt* und zählt konzeptionell zu den Kapitalmarktgleichgewichtsmodellen der "neoklassischen" Finanzierungstheorie. Das CAPM baut auf der Theorie der Wertpapiermischung (Portfoliotheorie von Harry M. Markowitz) auf, erweitert es um die Frage, welches das relevante Risikomaß für einzelne Anlageobjekte im Rahmen eines vollständig diversifizierten Portefeuilles ist und versucht auf dieser Grundlage zu erklären, wie risikobehaftete Anlagemöglichkeiten im Kapitalmarkt bewertet werden. Über sein Kernmodell, dem Modell der Wertpapierlinie, behauptet das CAPM eine positive, lineare Abhängigkeit der zu erwartenden Rendite einer Kapitalanlage von nur einer Risikoeinflussgröße (Ein-Faktor-Modell). Ziel des CAPM ist es letztlich, Konkurrenzgleichgewichtskurse (bzw. -renditen) für einzelne riskante Investitions- oder Finanzierungsprojekte (im Folgenden vereinfachend Wertpapiere genannt) im Portfolio- und Kapitalmarktzusammenhang unter Ungewissheit herzuleiten.

[* Vgl. dazu die Epoche machenden Arbeiten von William F. Sharpe: "Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk." The Journal of Finance 19, 1964, S. 425 – 442., John Lintner: "Security Prices, Risk and Maximal Gains from Diversification." The Journal of Finance 20, 1965, S. 587 ff. und von Jan Mossin: "Equilibrium in a Capital Asset Market." Econometrica, Vol. 34 (1966), S. 768 – 783.]

Modellprämissen

• Das CAPM in seiner ursprünglichen Version geht zunächst von den gleichen Voraussetzungen aus wie die Portfoliotheorie: Risikoaversion, beliebige Teilbarkeit der Wertpapiere, einperiodiger Planungszeitraum. Hinzu treten aus methodologischen Gründen arg vereinfachende Annahmen über den Kapitalmarkt und dessen Teilnehmer. Insbesondere wird unterstellt, dass sich der (einzige) Kapitalmarkt im Konkurrenzgleichgewichtszustand befindet: Der Markt befinde sich in einem Ruhezustand, unter dem niemand Anlass hat, sein Wertpapierportfolio umzuschichten. Die Anzahl der Wertpapiere ist hierbei fest vorgegeben und sämtliche Papiere werden gehalten.
• Des Weiteren besteht ein einheitlicher Marktzinssatz Rf, zu dem unbeschränkt finanzielle Mittel angelegt und Kredite aufgenommen werden können ("pure rate"). Der Zinssatz Rf soll unter der erwarteten Rendite E(Rm) des riskanten, risikoeffizienten Markportfolios M liegen. Die Existenz eines risikoeffizienten Marktportfolios seinerseits setzt unabdingbar informationseffiziente Kapitalmärkte voraus.
• Für alle Marktteilnehmer wird angenommen, dass sie streng-rationale Entscheidungen treffen, zudem die gleichen Erwartungen über künftige mögliche Renditen, Risiken und Kovarianzen der einzelnen Wertpapiergattungen hegen (homogene Erwartungen) und dass kein einziger Markteilnehmer bedeutend genug ist, diese Daten zu verändern. Alle Markbeteiligten sind im Sinne der Portfoliotheorie risikoavers. Ihre Bestrebungen richten sich darauf, den Risiko- und Konsumnutzen ihres Vermögens zum Ende der Planperiode zu maximieren.
• Der Kapitalmarkt ist frei von Friktionen. Es bestehen keine Handelskosten (Transaktionskosten), wie Börsengebühren, oder Steuern, und es bestehen fernerhin bei vollkommener Markttransparenz keine personellen, sachlichen oder sonstigen Präferenzen gegenüber anderen Marktbeteiligten. Es herrscht mithin vollkommener Wettbewerb ("Annahme vollkommener Märkte").

Modellkern

Aus vorstehenden Annahmen folgt, dass alle Kapitalanleger unabhängig von ihrem individuellen Grad der Risikoscheu ein in gleicher Weise zusammengesetztes risikobehaftetes Wertpapierportfolio auf der Grundlage der Portfoliotheorie von Markowitz bilden ("Tobin-Separation"). Dieses Portfolio trägt den Namen Marktportfolio M. In jenem Marktportfolio M sind sämtliche gehandelten Wertpapiere vorhanden, gewichtetet im Verhältnis zu ihren jeweiligen Marktwerten. Im μ/σ-Diagramm (vgl. die folgende Abbildung) repräsentiert das Tangentialportefeuille auf der vom Sicherheitszins Rf ("pure rate") ausgehenden Tangente an den Berührungspunkt der Effizienzlinie riskanter Wertpapiere ("efficient frontier") das Marktportfolio M. Das Tangentialportefeuille M ist damit zugleich das einzige Portefeuille auf der Effizienzlinie, das die Existenz dominanter Positionen ausschließt. Je nach Grad der Risikoaversion wird jeder rational entscheidende Anleger in einem nächsten Schritt seine bevorzugte ("nutzenmaximale") Positionierung auf der Kapitalmarktlinie wählen. Mit Ausnahme extrem risikoaverser Investoren, die ihre Mittel ausschließlich zu Rf investieren, wird jede individuell gehaltene Position (außer der des Marktportfolios selbst) abhängig vom Grad der Risikoscheu im optimalen Mischungsverhältnis sich aus einem entsprechenden Anteil des Marktportfolios M und aus einem entsprechenden Anteil der risikolosen Veranlagung zum Zinssatz Rf zusammensetzen. Die Struktur des in jeder risikoeffizienten Mischung enthaltenen Marktportefeuilles M selbst ist hierbei stets identisch. (Vgl. dazu: Erweiterung des Modells der Portfoliotheorie um eine sichere Anlagemöglichkeit und Tobin-Separation.)

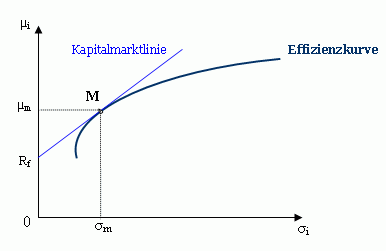
Abbildung: KapitalmarktlinieSind die erwarteten Kursänderungsraten und Risiken der einzelnen Wertpapiere bekannt, lässt sich auf einfache Weise auch die erwartete Rendite E(Rm) und das durch seine Standardabweichung ausgedrückte Risiko des Marktportfolios σm berechnen. Da Kapitalanlageentscheidungen in vielen Fällen auch eine wichtige Determinante der Finanzierungsmöglichkeiten von Unternehmungen bilden, wird die von Investoren erwartete Rendite des Marktportfolios E(Rm) in der Kapitalmarkttheorie aus einzelwirtschaftlicher Sicht als "Kapitalkosten unter Ungewissheit" bezeichnet. Demnach ist mit "Kapitalkosten unter Ungewissheit" stets eine prozentuale Größe und kein absoluter Kostenbetrag gemeint. "Kapitalkosten unter Ungewissheit" gestatten es einer Unternehmung im Kapitalmarktgleichgewicht, rationale Investitionsentscheidungen zu treffen, ohne hierbei zugleich ("simultan") dem Erfordernis einer Finanzierungsplanung zu unterliegen, indem kurzerhand die "Kapitalkosten unter Ungewissheit" als der maßgebliche Kalkulationszinssatz angesetzt werden. Dem Leitbild der Trennbarkeit gegenseitiger Abhängigkeiten über Märkte entsprechend lassen sich auf diese Weise unabhängig von den ansonsten obligatorischen Finanzierungskalkülen (und damit implizit auch unabhängig von den persönlichen Konsumpräferenzen des Disponierenden oder der Kapitalgeber) widerspruchsfreie Investitionsentscheidungen treffen ("Fisher-Separation"*). Die Zerlegung von Investitionsentscheidungen in Unternehmungen ebenso wie am Kapitalmarkt in jeweils delegierbare Einzelentscheidungen unter Wahrung der Interessen aller Marktbeteiligten wird dadurch erst möglich.

[* Vgl. dazu Fisher, Irving: "The Theory of Interest". New York 1930, S. 253 – 275.]

Um unter vorstehenden Modellannahmen in einer sonst institutionslosen Modellwelt eines Kapitalmarktes auf mathematisch-statistischem Wege den Kurs eines einzelnen im Marktportefeuille enthaltenen Wertpapiers im Kapitalmarktgleichgewicht herzuleiten, ist zunächst folgende Sprachregelung zu treffen:

Der Unterschied zwischen der erwarteten Rendite des Marktportfolios E(Rm) (= "Kapitalkosten unter Ungewissheit") und dem sicheren Zinssatz Rf wird "Marktpreis für das Risiko" genannt. Die Risikomenge eines jeden Wertpapiers in einem wohl diversifizierten Portfolio wird als Beta (ß) bezeichnet. Das Risiko des Marktportfolios M selbst wird auf 1 normiert, d.h. ßM = 1. Der ß-Faktor eines individuellen Wertpapiers i, βi, ist definiert als der Quotient aus der statistischen Kovarianz der Renditen zwischen dem betreffenden Wertpapier i und dem Marktportfolio M, (σim), zur Varianz der Renditen des Markt-Portfolios M, (σ²m), d.h.

βi = σim / σ²m .

Der Beta-Faktor bezieht sich ausschließlich auf das nicht weiter reduzierbare Risiko im Portfoliozusammenhang (das sogenannte systematische Risiko) und stellt damit zugleich den maßgeblichen Beitrag zum Portfolio-Risiko dar.

Nach einer sich hieran anschließenden formallogischen mathematisch-statistischen Optimumsbestimmung erhält man nun die zentrale Aussage des CAPM:

Die erwartete Rendite E(Ri) eines risikotragenden Investitionsobjekts i (wie z.B. eine Aktie i) setzt sich im Marktgleichgewicht zusammen aus dem Zinssatz Rf für finanziell risikolose Mittelanlagen und einer Risikoprämie. Die Risikoprämie ist das Produkt aus dem Marktpreis für das Risiko und der Risikomenge des betrachteten Investitionsobjektes i, die in ihrer Höhe durch ßi gemessen wird. Die formale Darstellung des CAPM als Renditegleichung ergibt den folgenden Ausdruck:

E(Ri) = Rf + [E(Rm) – Rf] · βi .

Vorstehender Ausdruck – aus dem sich zugleich das Modell der Wertpapierlinie ("security market line") herleitet – bildet die Kernaussage des CAPM und besagt: Der Beta-Faktor β ist das relevante Risikomaß für einzelne zu untersuchende Wertpapiere im Rahmen eines vollständig diversifizierten Portefeuilles. Je höher der Beta-Faktor eines Wertpapiers i wird, desto höher fällt seine erwartete Rendite E(Ri) aus und umgekehrt. Daraus folgt aber: Risikoaverse Investoren sind nur dann bereit, ein Wertpapier i mit einem hohen Risiko ßi zu halten, wenn hierfür im Markt eine angemessene Rendite zu erwarten ist.

Unter der gesetzten Annahme einperiodiger Planung lässt sich für jedes betrachtete Wertpapier die so berechnete Rendite auf einfache Weise in einen Gleichgewichtskurs überführen. Der Gleichgewichtskurs bzw. -rendite dient in diesem vereinfachten Erklärungsmodell der Marktpreisbildung als Maßstab dafür, inwieweit das untersuchte Wertpapier(portfolio) über den Markt im Einklang mit seinem Risiko bewertet wird, wobei wiederum von einer linearen Abhängigkeit zur Wertentwicklung des risikoeffizienten Marktportfolios ausgegangen wird.

• Kritische Würdigung des Capital Asset-Pricing-Modells (CAPM)

Das CAPM wurde in den 70er und 80er Jahren des letzten Jahrhunderts weiterentwickelt und verfeinert. So wurden insbesondere einzelne sehr realitätsferne Annahmen aufgehoben und geprüft, bis zu welchem Grad die Kernaussage des CAPM aufrechtzuerhalten ist. Es zeigte sich, dass auch unter weniger stringenten Annahmen das Modellergebnis weiterhin Bestand hat. Dies überrascht nicht, da die aus Modellen abgeleiteten Aussagen (Implikationen) zwangsläufig logisch wahr sein müssen, sofern kein logischer Denkfehler innerhalb des Modells vorliegt. Einer selbständigen empirischen Überprüfung indes entzieht sich das CAPM allein schon deshalb, weil sich das Markt-Portfolio aller Vermögenswerte nicht rekonstruieren lässt. Überdies vermag das CAPM unter den argen Modellvereinfachungen die Börsenkurse in der Realität nicht adäquat zu erklären, weil sich für reale Kapitalmärkte schwerlich ein Gleichgewichtszustand unter Ungewissheit postulieren lässt. Vielmehr zeigt es bloß die logischen Existenzbedingungen auf, unter denen sich Investitionsentscheidungen in Unternehmungen trennen lassen von den Finanzierungs- bzw. Konsumentscheidungen der Kapitaleigner.

Gangbar erscheint dagegen der Weg, aus den Modellergebnissen des CAPM passende Hypothesen über reale Kapitalmärkte zu formulieren, welche hieran anschließend an der Erfahrung (wenigstens vorläufig) zu verifizieren respektive zu falsifizieren sind. In einem solchen Versuch, Einsichten in nicht gleich offenkundige Zusammenhänge über die Wirklichkeit zu gewinnen, ist letztlich auch der Sinn des CAPM zu erblicken.

Autor: Bert H. Deiters

Herr Deiters ist Autor von dem Wissensbereich "Futures" : http://www.godmode-trader.de/wissen/futures/

World of Trading 2024: Triff die stock3-Experten live vor Ort

Am 22. & 23.11. findet die World of Trading in Frankfurt statt & stock3 ist mit dabei. Wir laden Dich ein, uns & unsere Experten näher kennenzulernen. Mit dabei sind u.a. Bastian Galuschka, Sascha Gebhard u.v.m.

Jetzt kostenloses Ticket sichern!