Square Root of 2 - Eine weitere Möglichkeit Potenziale und Korrekturen zu bemessen

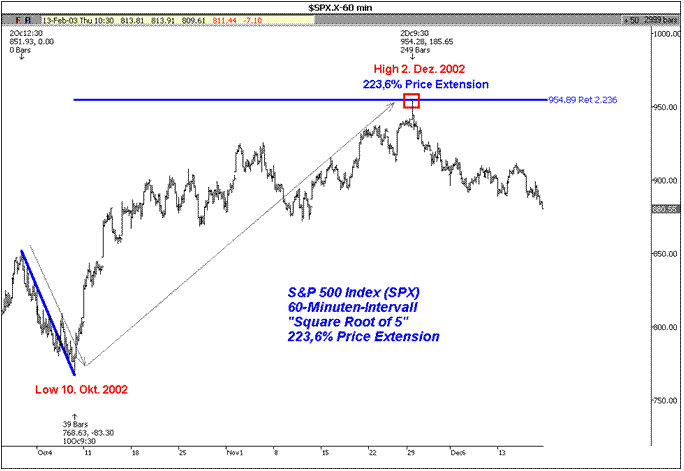
Am Beispiel des S&P 500 Index (SPX) konnten wir beobachten, wie der Index seine Rallye am 2. Dezember 2002 genau an der 223,6% Price Extension des Swings vom 2. Oktober 2002 zum Tief des 10. Oktober 2002 beendete, siehe Abbildung 1. Die Price Extension von 223,6% ist nichts anderes als die Bemessung des prozentualen Anteils eines entgegengesetzten Preisschwunges in Relation zur Range des vorangegangenen Preisschwunges mittels der Quadratwurzel aus 5 (√5 = 2,236).

Sie haben es sicherlich bereits gemerkt.

Wir veröffentlichen Charttechnik Lessons für Einsteigerniveau und Charttechnik Lessons für Fortgeschrittene. Dieses Lesson richtet sich wieder einmal an Fortgeschrittene.

Abbildung 1: S&P 500 Index (SPX), 60-Minuten-Intervall. Square Root of 5. 223,6% Price Extension. Der SPX beendet seine Rallye am 2. Dezember 2002 genau an der 223,6% Price Extension des Swings vom 2. Oktober 2002 zum Tief des 10. Oktober 2002.

Was hat die Quadratwurzel aus 5 mit den Finanzmärkten zu tun? Wir wissen bereits, dass die Verhältniszahl PHI = 1,618 (reziprok = 0,618) eine wichtige Rolle in den Finanzmärkten spielt. Zwischen PHI und der √5 oder 2,236 gibt es eine mathematische Beziehung, welche lautet:

√5 = j + j‘

wobei gilt: j = 1,618 und j‘ = 0,618

PHI lässt sich somit auch mit Hilfe der √5 ausdrücken:

j = (1 + √5) / 2

j‘ = (-1 + √5) / 2

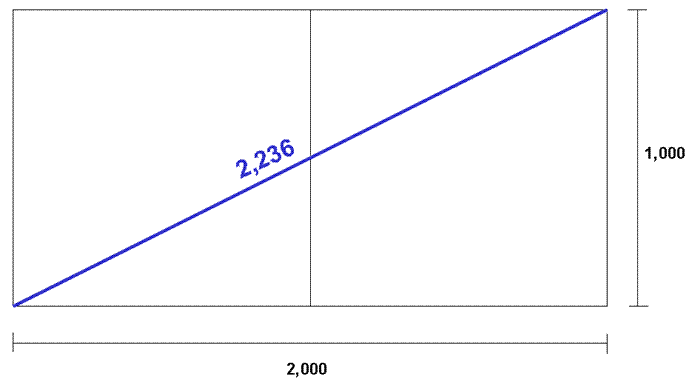
Weiterhin haben wir in der Lesson Square Root of 5 erfahren, dass sich die √5 in geometrischer Hinsicht als Diagonale zweier Quadrate, zum Beispiel eines Rechteckes mit einer Seitenlänge von 2 und einer Höhe von 1 ausdrücken lässt, siehe Abbildung 2.

Abbildung 2: Die vierte Dimension eines Quadrates. Diagonale zweier Quadrate = √5 = 2,236.

Nun stellt sich die Frage, ob es noch eine weitere Quadratwurzel gibt, deren abgeleitete Ratios auf die Finanzmärkte anwendbar sind? Es gibt sie. Dazu im weiteren Verlauf der Lesson mehr. Vorab erfolgt ein kurzer Exkurs, welcher die Bedeutung der philosophischen Geometrie für die Chartanalyse ansatzweise beschreibt.

Exkurs – Die Bedeutung der philosophischen Geometrie für die Chartanalyse

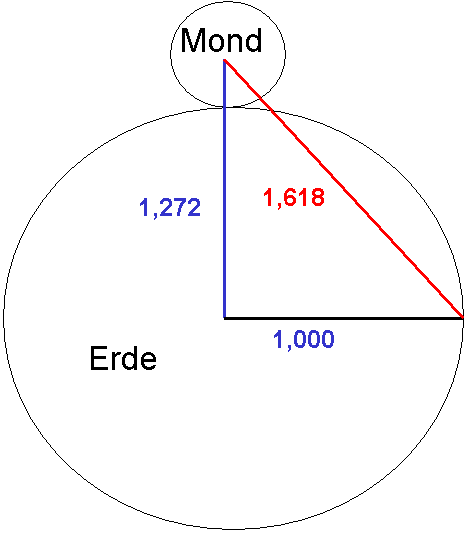
Die antiken Völker glaubten, dass die Natur eng mit den „heiligen“ Regeln der Geometrie verbunden war. Sie besaßen eine geometrisch-harmonische Vision einer universellen Ordnung des Universums, die sich nicht nur in den Pyramiden von Gizeh widerspiegelt, sondern beispielsweise in der Flora, der Fauna und in der Musik zu entdecken ist. Die Griechen besaßen Namen für wichtige Verhältniswerte, wie zum Beispiel PI für 3,1416 oder PHI für 1,618. Diese Zahlen repräsentieren die Instrumente für die Quadratur des Kreises. Dies sei deshalb erwähnt, weil die antike Geometrie von der Bemessung des Mondes und der Erde abgeleitet wurde, siehe Abbildung 3

Abbildung 3: Die antike Geometrie wurde von der Bemessung des Mondes gegenüber der Erde abgeleitet.

Falls Sie näher an dem Thema Geometrie interessiert sein sollten, so können Sie sich stapelweise Bücher kaufen, die all das detailliert beschreiben.

Fest steht, dass die komplette Elliott-Theorie und viele Gann-Theorien ihren Nährboden in dieser antiken philosophischen Geometrie fanden.

Warum diese Geometrie so einen essentiellen Effekt auf die Finanzmärkte hat, scheint mysteriös, braucht Sie aber nicht weiter zu kümmern, falls Ihnen das Ganze zu „esoterisch“ erscheint. Wichtig allein ist, dass die Geometrie in den Charts funktioniert, und das können Sie tagtäglich beobachten.

Für diejenigen, welche nach Gründen für den Zusammenhang zwischen philosophischer Geometrie und Chartanalyse suchen, sei erwähnt, dass sich die einzige Konstante in den Märkten, nämlich das Anlegerverhalten, nach einem bestimmten Naturgesetz dynamisch zu entwickeln scheint. Jede Welle eines Trends bildet komplementäre auf den Naturgesetzen basierende Patterns in irgendeiner strikten geometrischen Form, wie wir das schon in den Lessons „Fibonacci Price Retracements und Fibonacci Price Extensions I und II“ sowie in der Lesson „Square Root of 5“ beobachten konnten.

In der Antike lehrten zum Beispiel Gelehrte wie Platon oder Pythagoras eine dynamische Geometrie und Numerologie, mittels derer dynamische Formen entstehen. Während die klassische Geometrie von der

Form handelt, betrachtet die philosophische Geometrie das Sich-Entfalten jeder Form aus der vorigen Form. Wenn Sie diesen Ansatz der philosophischen Geometrie auf die Finanzmärkte übertragen, bedeutet dies, dass sich Chart Patterns hinsichtlich ihrer Proportion und ihren Ratios dynamisch fortsetzen.

Einige dieser Patterns sind prognostizierbar, andere wiederum nicht. Wenn Sie ein geometrisches Pattern identifizieren - und dazu werden wir in späteren Lessons noch kommen - dann können Sie den Markt sehr nahe an dem berechneten Wendepunkt betreten und ein enges Stop-Loss für ihre Position platzieren. Falls sich aus irgendeinem Grunde ihre Analyse als nicht genau das herausstellen sollte, was sie sich dachten, dann schließen Sie ihre Position schlechtestenfalls nur mit einem kleinen Verlust statt mit einem großen Verlust.

Später werden wir auch noch sehen, dass die Preis- und Zeitanalyse so etwas wie eine mathematische Annäherung an einen potenziellen Wendepunkt ist, und wir mittels dieses Ansatzes die Beziehungen zwischen Markthochs und -Tiefs auf der Zeit- und Preisamplitude gleichzeitig vergleichen können.

Square Root of 2 - Quadratwurzel aus 2

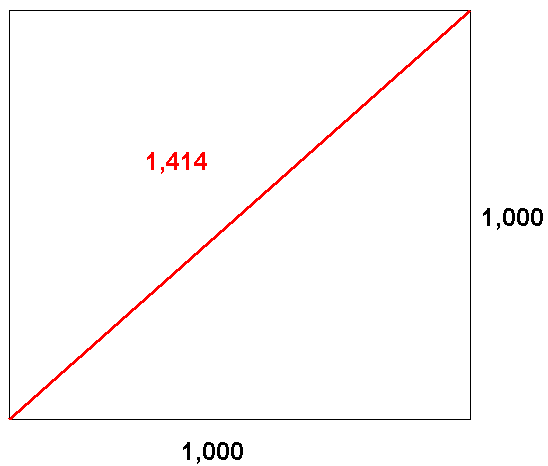
Abbildung 4: Quadratwurzel aus 2 = 1,414

Steht die Quadratwurzel aus 2 in Verbindung mit PHI, so wie das bei der Quadratwurzel aus 5 der Fall ist? Ja, sie tut es. Eine einfache Grafik soll dies verdeutlichen, siehe Abbildung 5.

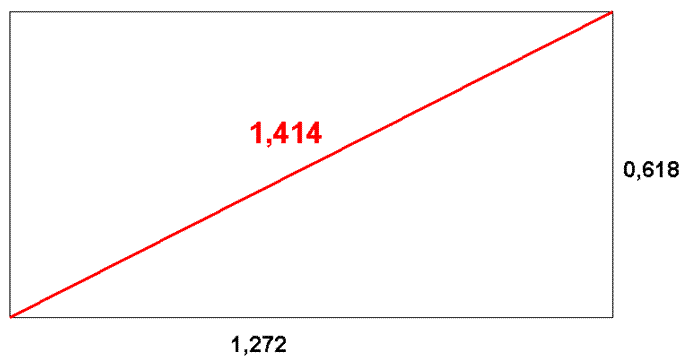
Abbildung 5: Diagonale eines Rechtecks mit den Seitenlängen 1,272 (= √PHI) und 0,618 (1 : PHI) beträgt 1,414 (= √2).

In der Abbildung sehen Sie, dass ein Rechteck, dass die Seitenlängen 1,272 (= √PHI) und 0,618 (1 : PHI) eine Diagonale von 1,414 ergibt. Auf mehrere Stellen nach dem Komma berechnet, gleicht die Quadratwurzel aus 2 ungefähr 1.414213562... Uns genügt der gerundete Verhältniswert von 1,414 beziehungsweise das Ratio von 141,4% für eine „Square Root of 2 Price Extension“. Der reziproke Wert der Quadratwurzel aus 2 (also 1 : √2) ergibt 0,707 beziehungsweise ein Ratio von 70,7% für ein „Square Root of 2 Price Retracement“. Der Verhältniswert von 0,7071 wird in der philosophischen Geometrie auch als „Heiliger Schnitt“ bezeichnet. Dieser heilige Schnitt lässt sich auch grafisch mittels einer Expansion eines Quadrates ermitteln, siehe Abbildung 6.

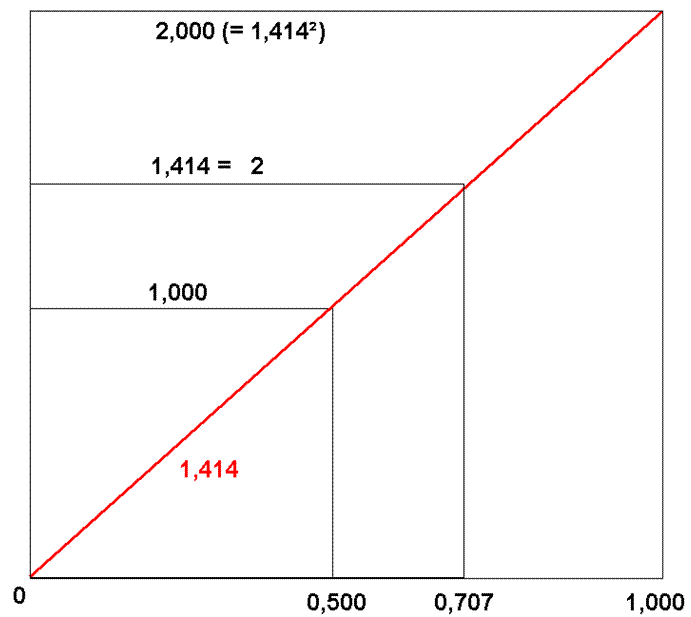
Abbildung 6: Harmonische Proportionen des Quadrates mit dem „Heilgen Schnitt“

In der Abbildung 6 sehen Sie die Expansion eines Quadrates mit den daraus abgeleiteten harmonischen Proportionen, darunter der „Heilige Schnitt“ (= 0,707). Mittels der Verwendung des Satzes des Pythagoras können wir die Länge der Diagonalen berechnen, die zur jeweiligen Seitenlänge eines Quadrates immer im Verhältnis 1,414 : 1,000 steht. Dieses Ratio wird immer das gleiche in jedem Quadrat sein.

An dieser Stelle sei erwähnt, dass es unter anderem diese harmonischen Ratios waren, die den legendären Trader W.D. Gann bei seinen Zeit-Preis-Analysen von Markttrends beschäftigten. Können Sie sich vorstellen, eine Art Quadratexpansion auf ein Chart anzuwenden? Vorab sei Ihnen gesagt, dass es so etwas gibt und das es sehr hilfreich ist, um Trading-Opportunitäten mit einem niedrigen Risiko bei gleichzeitig hoher Wahrscheinlichkeit zu identifizieren. Dies soll aber noch nicht hier erläutert werden, sondern in einer späteren Lesson, da die Materie relativ komplex ist und es einige Dinge zu beachten gilt.

Lassen Sie uns vorab einen Blick auf zwei einfache Chartbeispiele für die potenzielle Wirkungsweise des Square Roots of 2 ansehen:

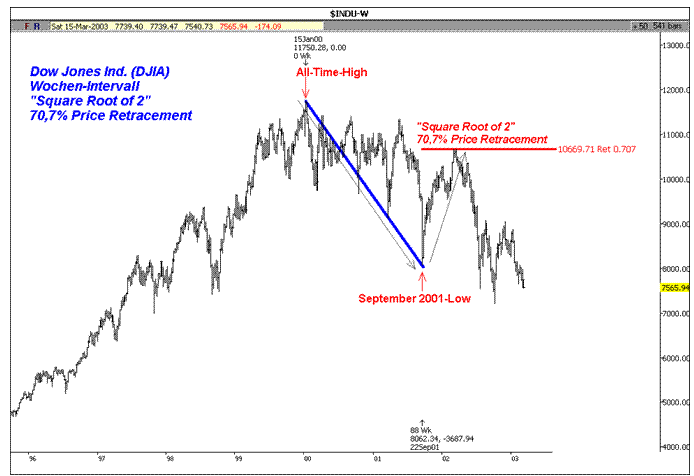
Abbildung 7: Dow Jones Industrial (INDU), Wochen-Intervall. „Square Root of 2“ 70,7% Price Retracement.

In der Abbildung 7 sehen Sie den Dow Jones Industrial (INDU) in einem Wochen-Intervall. Das Retracement der Abwärtsbewegung vom Allzeithoch bis zum Major Low des Septembers 2001 führt genau bis zum „Square Root of 2“ 70,7% Price Retracement. Eine Aufwärtsbewegung von ungefähr 2500 Punkten innerhalb von fast einem halben Jahr beendet also abrupt am „Heiligen Schnitt“ ihre Rallye. Danach fällt der Markt geradezu wie ein Stein.

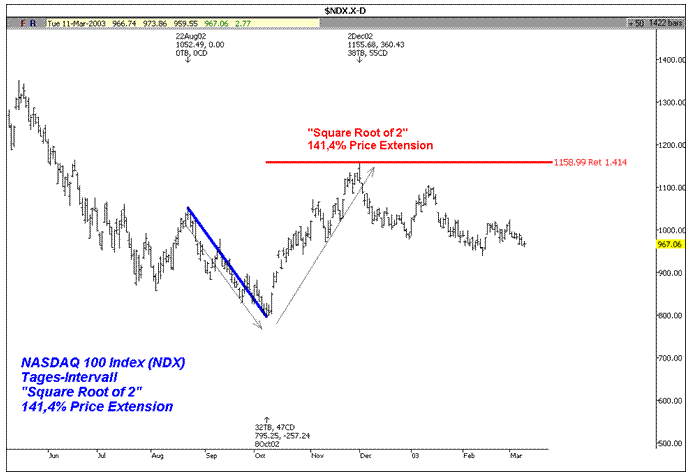
Abbildung 8: Nasdaq 100 Index (NDX), Tages-Intervall. „Square Root of 2“ 141,4% Price Extension

Im Chart sehen Sie den Nasdaq 100 Index (NDX) in einem Tages-Intervall. Das jüngste High des Marktes erschien am 2. Dezember 2002 an der „Square Root of 2“ 141,4% Price Extension des Swings vom 22. August 2002 zum Low des 8. Oktober 2002.

Nachdem wir uns in dieser Lesson den harmonischen Ratios eines Quadrates gewidmet haben, wenden wir uns im nächsten Teil dieser Reihe der dritten Dimension des Quadrates zu.

...Fortsetzung folgt....

Autor: Frank Thönnißen - Co-Investment Advisor bei STRADIVARI (Luxemburg)

http://www.trading-lehrgang.de

Welche Charttechnik & Trading Bücher kann ich kaufen ? Das-sind-meine-Lieblingsbuecher-Charttechnik-und-Trading

World of Trading 2024: Triff die stock3-Experten live vor Ort

Am 22. & 23.11. findet die World of Trading in Frankfurt statt & stock3 ist mit dabei. Wir laden Dich ein, uns & unsere Experten näher kennenzulernen. Mit dabei sind u.a. Bastian Galuschka, Sascha Gebhard u.v.m.

Jetzt kostenloses Ticket sichern!